تمارين عن قانون أوم
تم التدقيق بواسطة: فريق أراجيك
يُعرف قانون أوم على أنّه أحد المبادئ الأساسية في الكهرباء، لذا إن كنت من محبي تحليل ودراسة الدوائر الكهربائية تابع معنا للتعرف على هذا القانون، وحل بعض التمارين المساعدة في فهمه.
قانون أوم
يعتبر قانون أوم واحد من أهم قوانين الدوائر الكهربائية، فهو يشير إلى العلاقة بين التيار الكهربائي المار في دارة كهربائية أو أحد عنصرها وفرق الجهد المطبق في تلك الدارة أو على ذلك العنصر، إذ ينص القانون على أنّ التيار يتناسب تناسب طردي مع الجهد، لكن على شرط أن تبقى جميع الظروف الفيزيائية ودرجة الحرارة ثابتة، ذلك حسب ما وصل إليه العالم الفيزيائي الألماني جورج سيمون أوم بعد عدة تجارب، لذا سمّي القانون على اسمه.
يمكن التعبير رياضيًا عن علاقة قانون أوم بالعلاقة التالية:
V = I * R
حيث R تعبر عن ثابت التناسب بين الجهد والتيار، وهي مقاومة العنصر أو مكونات الدارة لتدفق التيار عبرها، وتقاس بوحدة الأوم التي يُرمز لها بالرمز (Ω).
يشتق من العلاقة السابقة معادلتين رياضيتين لحساب كل من التيار والمقاومة، وفق الآتي:
- العلاقة المعبرة عن التيار وفق قانون أوم:
I = V / R
- العلاقة المعبرة عن المقاومة وفق قانون أوم:
R = V / I
كما ذكرنا سابقًا، جميع العلاقات تنطبق فقط عندما تكون درجة الحرارة والظروف الفيزيائية ثابتة، حيث يمكن في بعض العناصر مثل المصباح الكهربائي المتوهج أن تسبب زيادة التيار ارتفاعًا في درجة الحرارة، لذا لا يمكن تطبيق قانون أوم في هذه الحالة ويمكننا القول أنّ المصباح الكهربائي المتوهج ينتهك قانون أوم.[footnote]Ohm's Law، من موقع: byjus.com، اطّلع عليه بتاريخ February/24/2021 | 06:43 AM[/footnote]
مثلث قانون أوم
يفيد قانون أوم في تحليل الدوائر الكهربائية، لذا يستخدم بكثرة في دراسة الكهرباء والإلكترونيات، لكن بالنسبة للذين يعانون من مشاكل في حفظ القوانين الرياضية فقد تم صياغة تقنية لتذكر القانون، وهي: رتب الحروف V المعبر عن الجهد، وI المعبر عن التيار، وR المعبر عن المقاومة في مثلث مثل الشكل التالي:
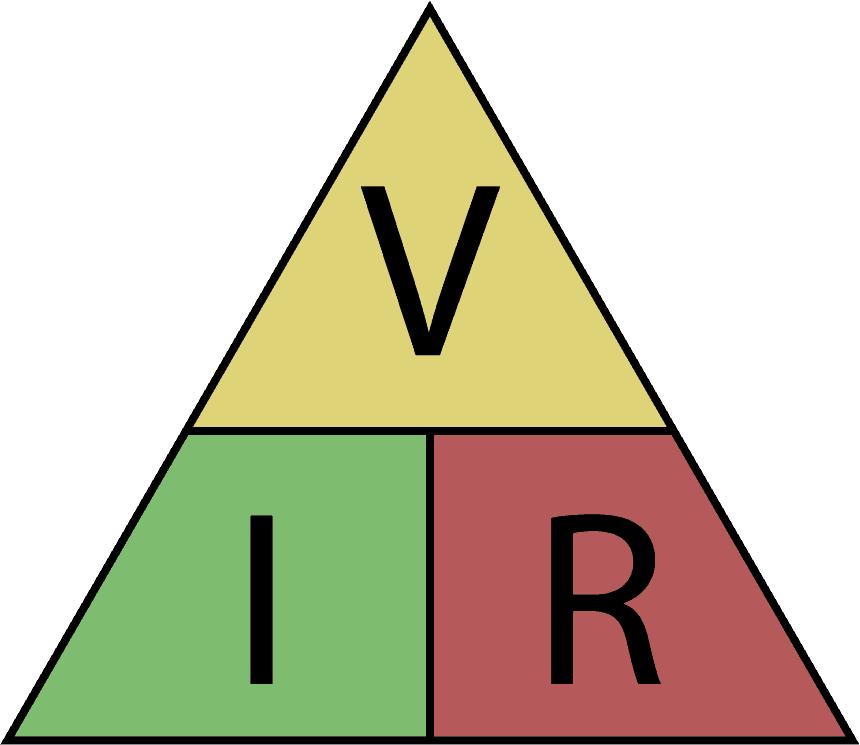
ففي حال كان معلومًا قيم التيار والجهد والمطلوب حساب قيمة المقاومة، فقط نحذف R من الشكل وما تبقى سيعبر عن العلاقة بالشكل:
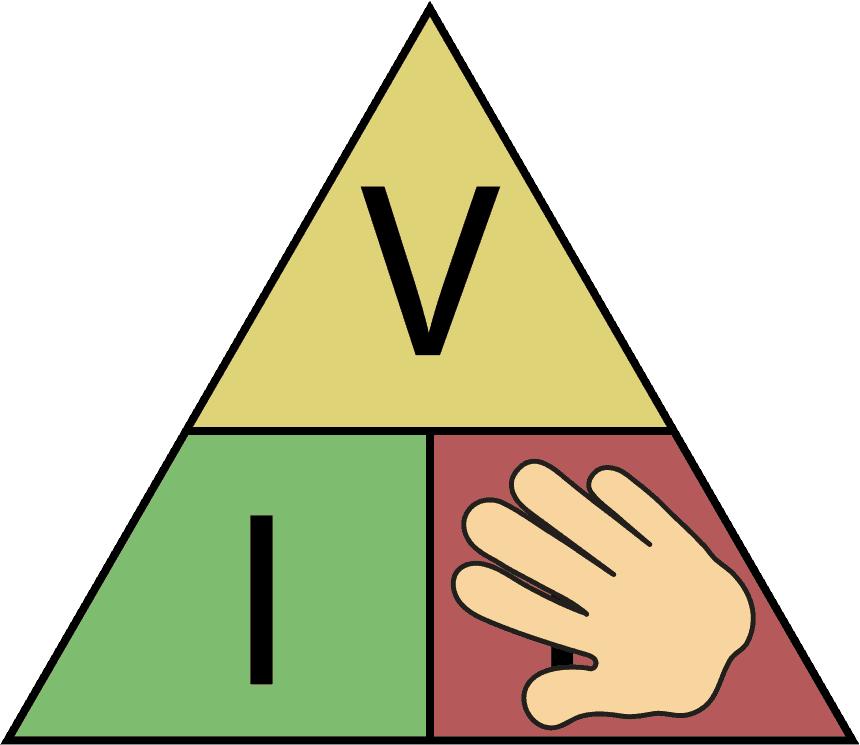
وفي حال كان معلومًا الجهد والمقاومة والمطلوب حساب قيمة التيار، نحذف I وما تبقى سيعبر عن العلاقة بالشكل:
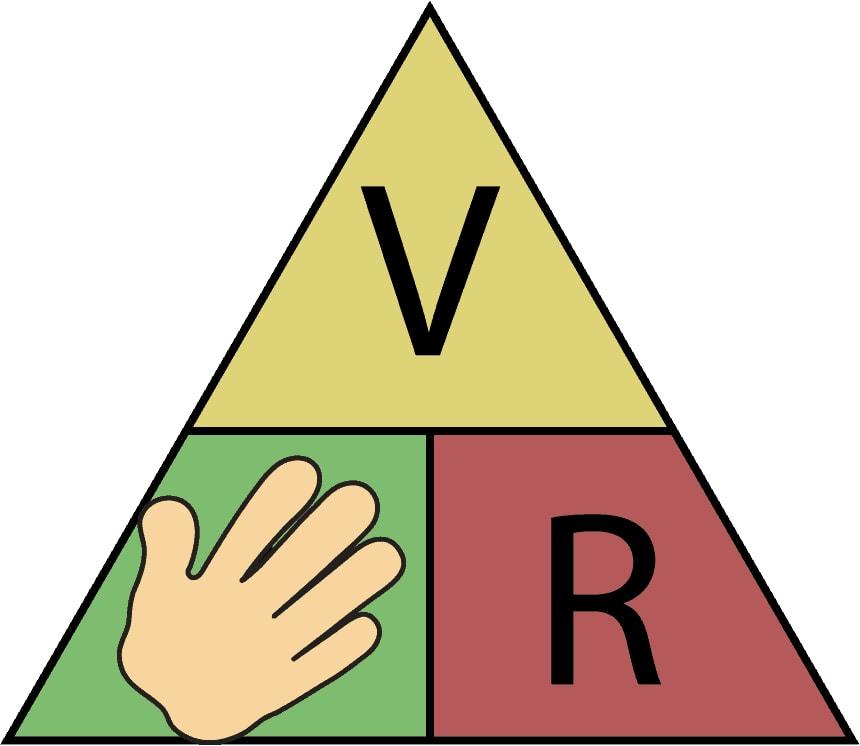
وفي حال كان معلومًا التيار والمقاومة والمطلوب حساب قيمة الجهد، نحذف V وما تبقى سيعبر عن العلاقة بالشكل:
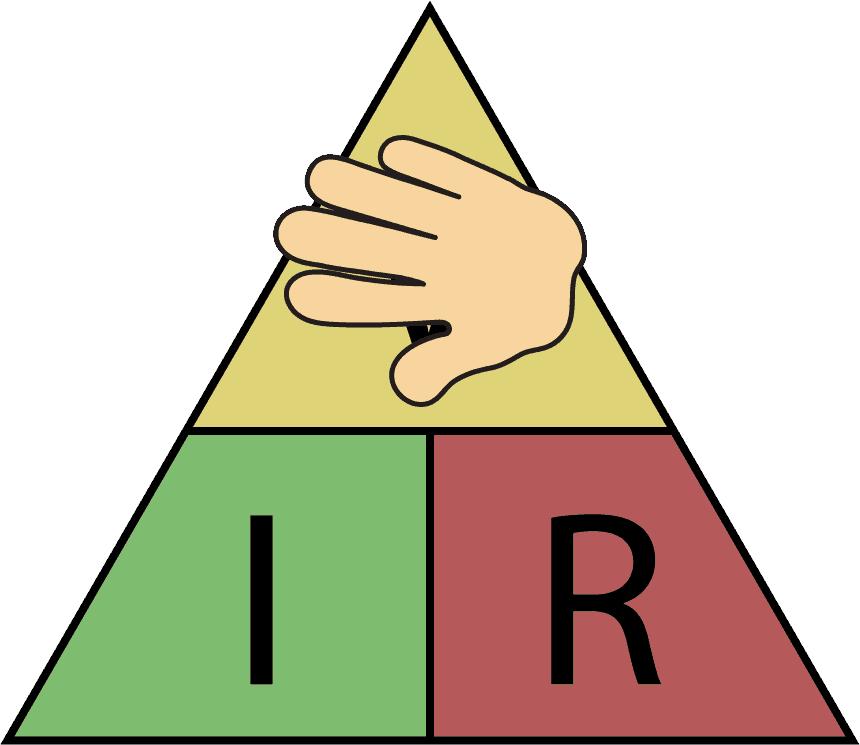
لكن لا بدّ من معرفة القوانين الجبرية لدراسة الكهرباء والإلكترونيات بجدية، ففي تلك الحالة لا بتطلب الأمر سوى حفظ الصيغة العامة للقانون (V = IR) واشتقاق الصيغتين الأخرتين منها عند الحاجة لهما.[footnote] Ohm’s Law - How Voltage, Current, and Resistance Relate ، من موقع: www.allaboutcircuits.com، اطّلع عليه بتاريخ February/24/2021 | 06:43 AM[/footnote]
تمارين عن قانون أوم
فيما يلي سنوضح بعض التمارين العملية لقانون أوم بصيغه الثلاث:
- مثال (1):
في الشكل الموضح ادناه، نجد دارة كهربائية مكونة من مصدر جهد كهربائي قيمته 12 فولت ومقاومة قيمتها 600 أوم، احسب قيمة التيار المتدفق في الدارة.

لحساب قيمة التيار، من مثلث قانون أوم نستنتج العلاقة المعبرة للتيار وهي:
I = V / R
بتعويض قيم الجهد والمقاومةفي العلاقة السابقة نجد:
I = 12 / 600 = 0.02 A
أي أنّ قيمة التيار تساوي إلى 0.02 أمبير أو 20 ميلي أمبير.
- مثال (2):
في الشكل الموضح أدناه، لدينا دارة كهربائية مكونة من مقاومة ذات قيمة 600 أوم ويمر عبرها تيار يساوي إلى 3 ميلي أمبير، احسب قيمة الجهد المطبق على الدارة.

لحساب قيمة الجهد، من مثلث قانون أوم نستنتج العلاقة المعبرة للجهد وهي:
V = R * I
بتعوبض قبم التيار والمقاومة في العلاقة السابقة نجد:
V = 600 * 3 = 1800 mV
أي أنّ قيمة الجهد المطبق على الدارة تساوي إلى 1800 ميلي فولت او 1.8 فولت.[footnote]How to Use Ohms Law، من موقع: www.build-electronic-circuits.com، اطّلع عليه بتاريخ February/24/2021 | 06:43 AM[/footnote]
- مثال (3):
ليكن لدينا المقاومة التالية ذات القيمة 1 أوم تتعرض المقاومة إلى انخفاض الجهد المطبق على طرفيها من 100 فولت إلى 10 فولت، احسب قيمة النيار المار خلال هذه المقاومة.
لحساب قيمة التيار المار عبر المقاومة نستخدم العلاقة التالية:
I = V / R
وبما أنّ المقاومة تتعرض لانخفاض جهد على طرفيها، تصبح العلاقة بالشكل:
I = (V2 - V1) / R
بتعويض المعاملات بقيمها نجد:
I = (100 - 10) / 1 = 90 A
- مثال (4):
في آخر التمارين عن قانون أوم لهذا المقال، لتكن لدينا المقاومة التالية ذات القيمة 10 أوم في دارة كهربائية، يمر فيها تيار قيمته تساوي إلى 2 أمبير، وجهد 120 فولت، احسب قيمة انخفاض الجهد على طرفي المقاومة.
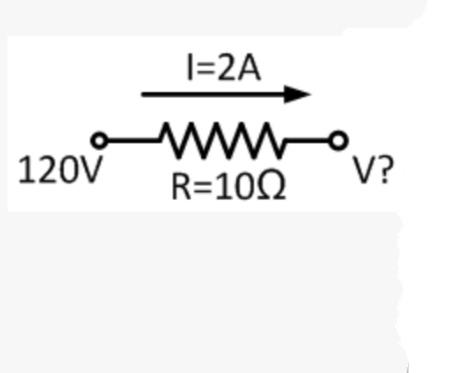
لحساب قيمة انخفاض الجهد نحسب بدايةً قيمة الجهد المستهلك في المقاومة باستخدام العلاقة:
V = I * R
بتعويض القيم نحصل على:
V = 2 * 10 = 20 V
وبالتالي تكون قيمة انخفاض الجهد الحاصل على طرفي المقاومة تساوي إلى حاصل طرح الجهد المستهلك في المقامة من الجهد على طرف المقاومة الأول، وفق الآتي:[footnote] Ohm’s law ، من موقع: eepower.com، اطّلع عليه بتاريخ February/24/2021 | 06:43 AM[/footnote]
V2 = V1 - V = 120 -2 =100 V
