حالات تشابه المثلثات
تم التدقيق بواسطة: فريق أراجيك
حالات تشابه المثلثات.. يمكننا القول عن جسمين أنّهما متشابهان عندما يكون لهما نفس الشكل بغض النظر عن تساوي حجميهما مع الأخذ بعين الاعتبار أنه حتى لو كان الجسمان باتجاهين مختلفين (تدوير بزاويةٍ معينةٍ) فهما يبقيان متشابهين، هذا يدل على أن الشكل هو الشيء الوحيد المهم عند تحديد ما إذا كان الجسمان متشابهين أم لا، والأمر بالتالي ينطبق على تشابه المثلثات في الرياضيات أيضًا.
عندما يتعلق الأمر بالمثلثات يمكننا ملاحظة أن جميع المثلثات متشابهةٌ لأنها تحتوي على نفس عدد الأضلاع والزوايا لكن التشابه يعد علاقةً خاصةً بين مثلثاتٍ محددةٍ فقط؛ فمن أجل القول إن المثلثين متماثلان يجب أن تتحقق بعض الشروط التي سنتعرف عليها فيما يلي، لكن في البداية سنطلع على أنواع المثلثات.[footnote]Geometry: Properties of Similar Triangles، من موقع: www.infoplease.com، اطّلع عليه بتاريخ February/09/2020 | 05:55 PM[/footnote]
ما هو علم المثلثات وما أهميته؟
هو فرع من الرياضيات يدرس الزوايا والمثلثات والتوابع المثلثية كالجيب والجيب التمام وهو أحد فروع علم الهندسة العامة يعتبر قدماء المصريين أول من عمل بقواعد حساب المثلثات، إذ استخدموها في بناء الأهرامات وبناء معابدهم الخلابة لكننا لا نعرف إلا القليل عم مدى علمهم إذ لم تصلنا مخطوطات كافية
ترجع معرفتنا بحساب المثلثات إلى الإغريق الذين وضعوا قوانينها ومن أهمها هي القائمة والحادة والمنفرجة يعتبر العلامة الفارسي نصير الدين الطوسي أول من اعتبر الحساب المثلثي فرعا مستقلاً عن علم النجوم. وقد وصلت معرفة الدوال المثلثية إلى أوروبا الغربية من خلال الترجمات إلى اللاتينية لأعمال كل من بطليموس وأعمال علماء الفلك الفرس والعرب من أمثال نصير الدين الطوسي والبتاني.
وكان عالم الرياضيات الهولندي جيما فريزنيوس هو أول من وصف طريقة التثليث و التي ما زالت مستعملة حاليا في علم المساحة إن علم المثلثات هو أساس الهندسة والبناء
متى يمكن أن نقول عن مثلثين أنهما متشابهان؟
يكون المثلثان متشابهين إذا كانت الزوايا المتقابلة من كل منهما متساوية أي عندما ينتج أحدهما عن الآخر بتكبيره أو تصغيره وتكون أطوال أضلاع المثلثين المتشابهين متناسبة أي إذا كان طول أقصر أضلاع المثلث الأول ضعف طول أقصر أضلاع المثلث الثاني فإن طول كل من الضلعين الأطول والمتوسط من المثلث الأول يكون ضعف طولي الضلعين الأطول والمتوسط من المثلث الثاني أيضاً وبالتالي فإن النسبة بين طولي الضلعين الأقصر والأطول في المثلث الأول مساوية للنسبة بين طولي الضلعين الأقصر والأطول في المثلث الثاني لكن هناك حالات أخرى قد يتشابه فيها مثلثان
أنواع المثلثات
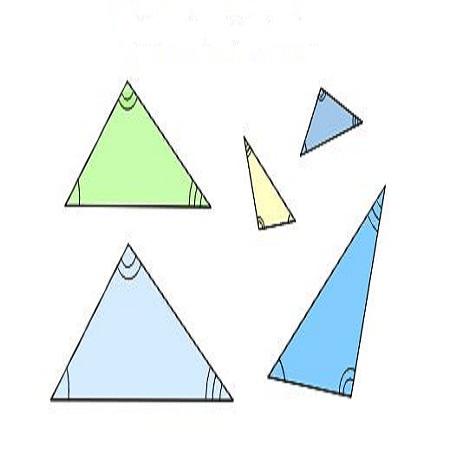
المثلثات هي عبارة عن أشكالٍ ثلاثيةٍ مغلقةٍ تتكون من ثلاثة رؤوسٍ وثلاثة أضلاعٍ وثلاث زوايا، بحيث يكون مجموع قياس الزوايا الثلاثة يساوي 180 درجةً. يتم تحديد نوع المثلث اعتمادًا على أطوال أضلاعه وقياس زواياه، فيكون لدينا الأنواع التالية:
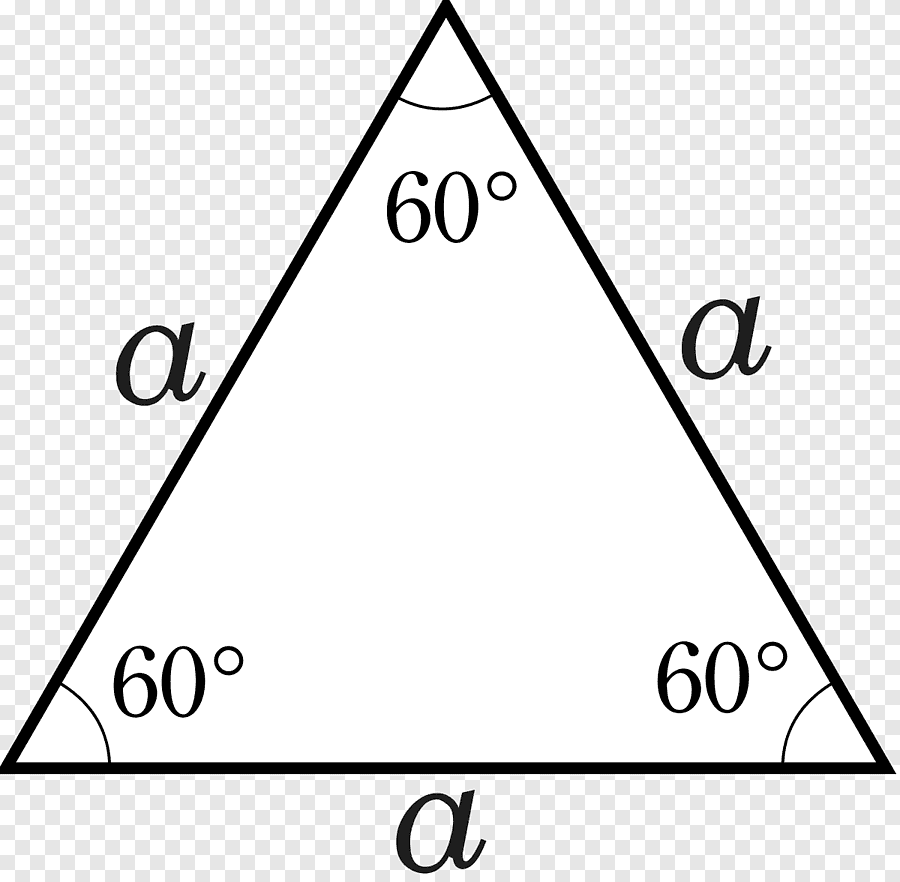
- المثلث متساوي الأضلاع: نقول عن مثلثٍ أنه متساوي الأضلاع عندما تكون أطوال أضلاعه وقياسات زواياه متساويةً جميعها، ويكون قياس كل زاويةٍ من زواياه 60 درجة.
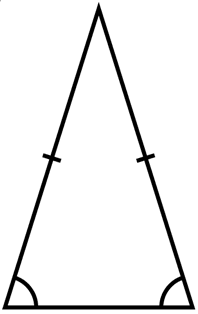
- المثلث متساوي الساقين: نقول عن مثلثٍ أنه متساوي الساقين عندما يكون له ضلعان فقط متساويان والزاويتان بين القاعدة والضلعين المجاورين متساويتان.
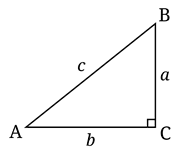
- المثلث قائم الزاوية: هو المثلث الذي تكون إحدى زواياه قائمة (90 درجة).
- المثلث مختلف الأضلاع: يكون المثلث مختلف الأضلاع عندما لا يوجد فيه أي أضلاعٍ أو زوايا متساوية مع بعضها البعض، نميز منه الأنواع التالية:
حالات تشابه المثلثات
لكي نقول عن مثلثين أنهما متشابهان يجب أن تتحقق إحدى الحالات التالية:
- تساوي قياس الزوايا
إذا كانت زاويتان من مثلثٍ تتساوى مع زاويتين مقابلتين من مثلثٍ آخر يمكننا القول أن المثلثين متشابهان، إذًا يكفي إثبات أن اثنين فقط من زوايا المثلثين متساويتان على التوالي لإثبات أن المثلثين متشابهان كون مجموع زوايا المثلث 180 درجةً بالتالي ستكون الزاوية الثالثة من الزوايا لكلا المثلثين متساويةً بشكلٍ تلقائيٍّ.
- تساوي طولي ضلعين وقياس الزاوية الواقعة بينهما
إذا كان طولا ضلعين من مثلثٍ متساويين مع طولي الضلعين المقابلين من مثلثٍ آخر، وكانت الزوايا الواقعة بين هذين الضلعين متساويةً مع الزاوية المقابلة من المثلث الآخر متساوية، فإنه يمكننا القول أن المثلثين متشابهان.
- تساوي أطوال الأضلاع الثلاثة
إذا كانت الأضلاع الثلاثة للمثلث الأول متساويةً في القياس مع أطوال أضلاع المثلث الآخر يكون المثلثان متشابهين.
- تساوي طولي وتري مثلثين قائمي الزاوية
إذا تساوى وتر مثلثٍ قائم الزاوية مع وتر مثلثٍ آخر قائم الزاوية أيضًا، وتساوى طول أحد الأضلاع الأخرى مع طول الضلع المقابل له من المثلث الآخر يكون المثلثان متشابهين.
مثال عن تشابه المثلثات
سنستعرض المثال التالي لبيان إحدى حالات التشابه السابقة، إذا كان لدينا ABC مثلث منفرج الزاوية، ولتكن لدينا القطعة المستقيمة AC الموازية للضلع AC، هل يمكننا القول عن المثلثين الواضحين في الشكل أنهما متشابهان؟
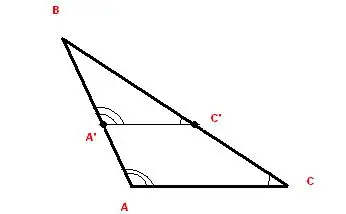
نعم بالتأكيد المثلثان متشابهان، يفسر ذلك بأن القطعة المستقيمة AC موازية للضلع AC، وبالتالي تكون الزاويتان BAC وBAC متطابقتين، وكذلك الزاويتان BCA وBCA متطابقتان، بالتالي بما أن المثلثين لهما زاويتان متساويتان فهما متشابهان وفق الحالة الأولى للتشابه.[footnote]Similar Triangles Examples and Problems with Solutions، من موقع: www.analyzemath.com، اطّلع عليه بتاريخ February/09/2020 | 05:56 PM[/footnote]
بعض الخصائص الهامة عن المثلثات المتشابهة
- يمكن الحكم في تشابه المثلثات بمجرد تشابها بالشكل دون النظر إلى حجمها.
- جميع المثلثات متساوية الأضلاع هي مثلثات متشابهة.
 TV
TV Partner With Us
Partner With Us