قانون حساب حجم الاسطوانة

تم التدقيق بواسطة: فريق أراجيك
خزانُ مياهٍ أو علبةُ طلاءٍ أو أنبوبُ اختبارٍ أو أي حاويةٍ تحتوي على مقطعٍ دائريٍّ وامتداد معين في الفضاء يطلق عليها الأسطوانة، فما هي الأسطوانة؟ وكيف يتم حساب حجم الاسطوانة ومساحتها السطحية؟[footnote]، How to Calculate the Capacity of a Cylinder ، من موقع: sciencing.com، اطّلع عليه بتاريخ 3-11-2019[/footnote]
أنواع الهندسة
قبل التحدث عن حجم الاسطوانة وخصائصها يجب أن نتعرف على الهندسة ثلاثية الأبعاد.
يمكن تقسيم الهندسة إلى نوعين:
- الهندسة المستوية.
- الهندسة الفراغية.
تتعامل الهندسة المستوية مع الأشكال ثنائية الأبعاد أو الأشكال المسطحة مثل الخطوط والمنحنيات والمضلعات وغيرها من الأشكال التي يمكن رسمها على قطعةٍ من الورق، أما الهندسة الفراغية فتهتم بدراسة الأشكال ثلاثية الأبعاد مثل الأسطوانات والمكعبات والكرات وغيرها من الأشكال التي يتم قياسها في 3 اتجاهات. الفرق الوحيد بين الأشكال الثنائية الأبعاد والأشكال ثلاثية الأبعاد هو وجود العمق أو الارتفاع، وتستخدم هذه الأشياء بشكلٍ كبيرٍ في حياتنا اليومية.
في الأشكال ثلاثية الأبعاد تسمى الأسطح المسطحة الوجوه، ويسمى الخط الذي يلتقي فيه وجهانٌ بالحافة والنقطة التي تلتقي فيها الحواف الثلاثة تسمى الرأس.[footnote]، Properties of Cylinder ، من موقع: byjus.com، اطّلع عليه بتاريخ 3-11-2019[/footnote]
الاسطوانة
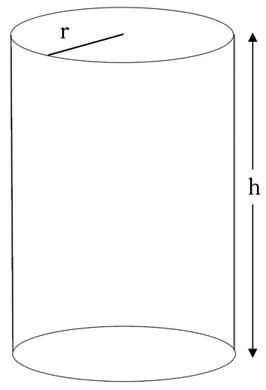
هي مجسمٌ هندسيٌّ شائعٌ جدًا في الحياة اليومية، له نهايتان دائريتان تسميان القواعد، وتكونان دائمٍا متطابقتين ومتوازيتين، وإذا قمنا بفك الاسطوانة فسنجد أن جانبها عبارةٌ عن مستطيلٍ. وللأسطوانة عدة مصطلحاتٍ مرتبطة بها وهي:
- ارتفاع الاسطوانة (h): وهو المسافة العمودية بين القواعد.
- نصف قطر الأسطوانة (r): وهو نصف قطر إحدى قواعد الأسطوانة الدائرية.
- محور الأسطوانة: هو الخط الذي يصل بين مركز قاعدتي الاسطوانة.[footnote]، Cylinder
، من موقع: www.mathopenref.com، اطّلع عليه بتاريخ 3-11-2019[/footnote]
بعض خصائص الاسطوانة
- قاعدتا الاسطوانة دائمًا متطابقتان ومتوازيتان.
- إذا كانت قاعدة الأسطوانة ذات شكلٍ بيضاويٍّ فيُطلق عليها بأسطوانةٍ بيضاوية الشكل.
- إذا كانت نقطة تتحرك على مسافةٍ ثابتةٍ من المحور يتم إنتاج أسطوانة دائرية.
- تشبه الأسطوانة المنشور نظرًا لوجود المقطع العرضي نفسه في كل مكانٍ.
- إذا لم تكن الاسطوانة قائمةً، وكان المحور يميل على القاعدة نحو اليمين تُسمى باسطوانة يمنى، ويكون طول المحور مساويًّا لارتفاع الاسطوانة مقسومًا على جيب زاوية الانحراف.
كيف حساب حجم الاسطوانة
يعبر عن حجم الاسطوانة بالعلاقة التالية:
V = π r2 h أي مساحة القاعدة * الارتفاع
- حساب نصف القطر
أول خطوةٍ في حساب حجم الاسطوانة هي إيجاد نصف قطر قاعدة الأسطوانة الدائرية، إذا كان قطر الدائرة معروفًا فما علينا سوى تقسيمه على 2، أما إذا كان المحيط معروفًا فيمكن تقسيمه على 2π للحصول على نصف القطر، إذا لم يكن أي منها معروف فيمكن استخدام المسطرة لقياسه. - حساب مساحة القاعدة الدائرية
للقيام بذلك نقوم بتعويض نصف القطر بعلاقة مساحة الدائرة: π r2
حيث π تمثل قيمته 3.14 - حساب ارتفاع الاسطوانة
إذا كان الارتفاع معروفًا يمكن الاستمرار في حساب حجم الاسطوانة لكن إذا لم يكن كذلك فيمكن استخدام المسطرة لقياسه. - حساب حجم الاسطوانة
لحساب الحجم نقوم بضرب مساحة القاعدة بالارتفاع، ويتم دائمًا تحديد الإجابة النهائية بوحداتٍ مكعبةٍ.[footnote]، How to Calculate the Volume of a Cylinder، من موقع: www.wikihow.com، اطّلع عليه بتاريخ 3-11-2019[/footnote]
مثال لحساب حجم الاسطوانة
إذا كان لدينا أسطوانة نصف قطرها 8 سم وارتفاعها 15 سم، احسب حجم الاسطوانة .
الحل:
نقوم بتبديل المعطيات في علاقة الحجم:
V = π r2 h= 3.14 * 82 * 15 = 3014.4 cm3
أي حجم الاسطوانة حوالي 3014 سم مكعب.
برنامج لحساب الحجم
أدخل نصف قطر الاسطوانة
أدخل طول الاسطوانة
كيف حساب المساحة السطحية الكلية للأسطوانة
المساحة السطحية لشكلٍ ما هي مجموع مساحة كل وجوهه، لحساب مساحة الأسطوانة الجانبية يجب حساب مساحة قواعدها وإضافة ذلك إلى مساحة جدارها الخارجي.
تعطى صيغة مساحة الاسطوانة الكلية بالعلاقة:
S = 2πr2 + 2πrh
- حساب مساحة القواعد الدائرية:
S1 = 2πr2
لحساب مساحة القواعد الدائرية نحتاج لتحديد قيمة نصف قطر القاعدة r، إذا كان قطر الدائرة معروفًا فما علينا سوى تقسيمه على 2، أما إذا كان المحيط معروفًا فيمكن تقسيمه على 2π للحصول على نصف القطر، إذا لم يكن أي منهما معروفًا فيمكن استخدام المسطرة لقياسه.
بعد معرفة قيمة نصف القطر نقوم بتعويضه بالعلاقة السابقة وتعويض قيمة π بـ 3.14
- حساب مساحة السطح الجانبي للأسطوانة:
S2 = 2πrh
نحسب أولًا محيط القاعدة الدائرية وفق العلاقة:
A = 2πr
بتعويض نصف القطر بالعلاقة نحصل على المحيط.
نقوم بضرب الارتفاع h بمحيط القاعدة الدائرية للحصول على مساحة السطح الجانبي للأسطوانة:
S2 = A*h
بعد حساب كل من مساحة القواعد الدائرية ومساحة السطح الجانبي للأسطوانة نقوم بجمع المساحتين للحصول على المساحة السطحية الكلية للأسطوانة، وتقاس بوحداتٍ مربعةٍ.[footnote]، Volume of a Cylinder ، من موقع: www.varsitytutors.com، اطّلع عليه بتاريخ 3-11-2019[/footnote]
S = S1 + S2
مثال لحساب المساحة السطحية للأسطوانة
إذا كان لدينا أسطوانة نصف قطرها 3 سم وارتفاعها 10 سم، احسب مساحة الاسطوانة الكلية.
الحل:
أولاً: حساب مساحة القواعد الدائرية بتبديل قيمة نصف القطر r بالعلاقة التالية:
S1 = 2πr2
2(3) (3.14) 2 =
56.52cm2 =
ثانياً: حساب محيط القاعدة الدائرية:
(3) (3.14) 2 = A = 2πr
11.42cm =
ثالثاً: حساب مساحة السطح الجانبي للأسطوانة:
10 * 11.42 = S2= 2πrh
114.2cm2 =
رابعاً: حساب المساحة السطحية للأسطوانة:
S = S1 + S2
114.2 + 56.52 =
170.72cm2 =
أي مساحة الاسطوانة الكلية حوالي 171 سم مربع.
