ما هي معادلة شرودنجر؟
تم التدقيق بواسطة: فريق أراجيك
معادلة شرودنجر هي معادلة تفاضليّة خطيّة تصف دالة الموجة 𝚿 وتُعتبر المعادلة الأساسيّة لعلم الظواهر دون المجهريّة المعروفة بميكانيكا الكم، ولها نفس الأهميّة المركزيّة لقوانين نيوتن للحركة بالنّسبة للظواهر واسعة النطاق في الميكانيكا الكلاسيكيّة.
أبصرت معادلة شرودنجر النور (Schrodinger equation) في عام 1926 على يد عالم الفيزياء النمساوي إريون شرودنجر (1887-1961)، الذي فاز بجائزة نوبل مع بول ديراك في عام 1933 لمساهماتهما في فيزياء الكم. وقد أرست هذه المعادلة أسس علم ميكانيكا الكم الذي يُعنى بدراسة حركة الجسيمات الذرية، ودون الذرية، وتماثل هذه النظرية في أهميتها قوانين نيوتن في الميكانيك الكلاسيكي.
ميكانيك الكم
ويُعرف ميكانيك الكم بأنّه علمٌ يتعامل مع سلوك المادة والضوء على النّطاق الذّري ودون الذّري، ويحاول وصف خصائص الجزيئات والذرات ومكوناتها كالإلكترونات، والبروتونات، والنيوترونات، وغيرها من الجسيمات الباطنيّة؛ مثل الكواركات والغلونات. وتتضمن هذه الخصائص تفاعلات الجسيمات مع بعضها البعض ومع الإشعاع الكهرومغناطيسي (أي الضوء والأشعة السينية وأشعة جاما).
عواقب نظرية الكم
غالباً ما يبدو سلوك المادة والإشعاع على النطاق الذري غريباً؛ وبالتّالي يَصعُب فهم وتصديق عواقب نظرية الكم، وكثيراً ما تتعارض مفاهيمها مع مفاهيم الفطرة السليمة المستمدّة من ملاحظات العالم الحقيقي؛ ومع ذلك فإنّه لا يوجد سبب يؤدي إلى أنّه يجب أن يتوافق سلوك العالم الذّري مع سلوك العالم المألوف الواسع النّطاق، ومن المهم إدراك أنّ ميكانيكا الكم هو فرع من أفرع الفيزياء، وأنّ عمل الفيزياء هو وصف ومحاسبة طريقة العالَم (في كل من النطاق الكبير والصغير) كما هو في الواقع وليس كيف يمكن أن يتخيله المرء أو يرغب أن يكون.
في الأساس تُعتبر معادلة شرودنجر معادلة (دّالة) موجيّة، تصف شكل الموجات الاحتماليّة (أو وظائف الموجة) الّتي تحكم حركة الجسيمات الصّغيرة، وتحدد كيف تتغير هذه الموجات بالتّأثيرات الخارجيّة.
وتُعبّر الدالة الموجيّة عن كميّةٍ متغيرةٍ، وتكون قيمتها بالنسبة لجسيّم موجود في زمان ومكان محددين متعلّقة باحتماليّة تواجده في تلك النقطة في زمنٍ محدد، ويكثُر استخدام مصطلح الدّالة الموجيّة في ميكانيك الكم.
خصائص الدّالة الموجيّة
توفر جميع المعلومات القابلة للقياس حول الجسيّم.
𝚿 يجب أن يكون مستمراً وذو قيمة فرديّة.
باستخدام معادلة شرودنجر تصبح حسابات الطاقة سهلة.
تُوزع الاحتمالات في ثلاثة أبعاد باستخدام الدّالة الموجيّة.
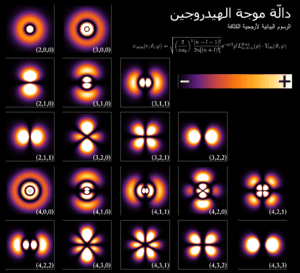
تحقّقَ شرودنجر من صحة المعادلة بتطبيقها على ذرة الهيدروجين، وتوقّع العديد من خصائصها بدقة ملحوظة حتى أصبحت المعادلة تُستخدم على نطاق واسع في الفيزياء الذريّة والنوويّة والصلبة.
معادلة شرودنجر والتطور الزمني لوظيفة الموجة
بمساعدة معادلة شرودنجر التّي تعتمد على الوقت، تمَ توفير التّطور الزمني لوظيفة الموجة، ويصبح من السهل فهم النّظام باستخدام وظيفة الموجة بالنّسبة للجسيّم في المجال المحافظ لنظام القوة، ويمكن بسهولة حساب طاقة الجسيّم، ويمكن إيجاد التّوزع المحتمل في الأبعاد الثلاثة عن طريق هذه الدالة الموجيّة.
عبّر شرودنجر عن فرضيّة دي بروجلي فيما يتعلق بسلوك الموجة للمادة بشكلٍ رياضيّ قابل للتّكيف مع مجموعةٍ متنوعةٍ من المشّاكل دون افتراضات اعتباطيّة إضافيّة، وقد اعتمدَ على صياغةٍ رياضيّةٍ، حيث يمكن اشتقاق انتشار الخط المستقيم لأشعة الضوء من حركة الموجة؛ عندما يكون الطول الموجي صغيراً مقارنة بأبعاد الجهاز المستخدم؛ وبنفس الطريقة بدأ شرودنجر في إيجاد معادلة موجيّة للمادة تعطي انتشاراً يشبه الجسيمات عندما يصبح الطول الموجي صغيراً نسبياً، ووفقاً للميكانيكا الكلاسيكيّة، إذا تعرّض جزء من كتلة (me) لقوة بحيث تكون طاقتها المحتملة V (x,y,z)، في الموضع (x ، y ، z )، ثم يكون مجموع V (x, y, z) والطاقة الحركية p2 / 2me تساوي ثابتاً وهو إجمالي الطاقة E للجسيّم.
استخدامات معادلة شرودنجر
معادلة شرودنجر والتي يطلق عليها أيضًا (المعادلة الموجية) هي أساسًا معادلة تفاضلية، تصف طاقة الإلكترون وموقعه في المكان والزمان وتعبر عنها بصورة رياضية، وتقوم على ثلاثة أسس هامة: معادلة الموجة المستوية، فرضية برولي حول موجة المادة، مبدأ حفظ الطاقة.
كما تبحث هذه المعادلة في شكل الأمواج التي تُحدد حركة الجسيمات الصغيرة، وتفسِّر بوضوح تأثير العوامل الخارجية على تلك الأمواج، وتقدّم معلومات حول سلوك الإلكترون المرتبط بالنواة بالاستناد إلى مبدأ حفظ الطاقة. بتطبيق هذه المعادلة على ذرة الهيدروجين تمكّن شرودنجر من إثبات صحتها، وحدّد خصائص متعددة لذرة الهيدروجين، واستخدمت هذه المعادلة على نطاق واسع في الفيزياء الذرية والنووية.
أنواع معادلة شرودنجر
يوجد نوعان لمعادلة شرودنجر (معادلة شرودنجر المعتمدة على الزمن – معادلة شرودنجر غير المعتمدة على الزمن)
معادلة شرودنجر المعتمدة على الزمن (Time-dependent Schrödinger equation) :
iℏ d/td ∣Ψ(t)⟩= H ^ ∣Ψ(t)⟩
Ψ = دالة موجية تعتمد على الوقت
ℏ: ثابت بلانك
i = وحدة تخيلية
H ^= عامل هاميلتوني
معادلة شرودنجر غير المعتمدة على الزمن (Time-independent Schrödinger equation):
E ^H^ = H Ψ
H ^= عامل هاميلتوني
E: ثابت التناسب
تبعًا لمعادلة شرودنجر المعتمدة على الزمن يمكن أن تشكل الدالات الموجية موجات ثابتة (الحالات الثابتة)، والتي إذا تم تصنيفها وفهمها، يمكن بسهولة حل معادلة شرودنجر المعتمدة على الزمن لأي حالة، في حين تُستخدم معادلة شرودنجر غير المعتمدة على الزمن فقط لوصف الحالات المستقرة عندما لا يكون العامل الهاميلتوني معتمدًا على الزمن، وبذلك تكون معتمدة فقط على المكان.
من خلال حساب معادلة شرودنجر (الدّالة الموجية) يمكن أن نحصل على معلومات عن الجسيم القابل للقياس، حساب طاقته، إيجاد التوزع المحتمل له في الأبعاد الثلاثة، كما يمكن تقدير القيمة المتوقعة لمتغير محدد.
تتميز الدالة الموجية بكونها ذات قيمة مفردة دوَمًا، فإذا كان قيمة مربعها مساوية للواحد فإن احتمال اكتشاف وجود جسيم في مكان ما تساوي الواحد أيضًا، كما يسهل فهم نظام القوة لدى تطبيق الدّالة الموجية على جسيمٍ موجودٍ في مجالٍ مُغلقٍ ضمن هذا النظام
ولمعادلات شرودنجر دور مهم في نمذجة الظواهر الفيزيائية كما أنها تمثِّل كائنًا رياضيًا مهمًا، وهي مجال واسع للأبحاث منها تلك التي تركز على فهم الروابط بين المعادلات من نوع شرودنجر وبعض الظواهر الفيزيائية مثل ديناميات الدوامة في الموائع والسوائل الفائقة، وكذلك انتشار الإشارات في الأسلاك الكمومية.
 LEAP26
LEAP26 ASUS
ASUS RØDE
RØDE REDMAGIC
REDMAGIC TV
TV Partner With Us
Partner With Us