الاعداد العقدية او الاعداد المركبة

تم التدقيق بواسطة: فريق أراجيك
الاعداد العقدية او الاعداد المركبة هي الأعداد التي تحمل الصيغة الرياضية a+ib؛ حيث أنّ a وb، عددان حقيقيّان، وقيمة i هي جذر العدد -1؛ وهي عبارةٌ عن رقمٍ وهميٍّ يطلق عليه Iota، وبذلك يقسم العدد المركب إلى جزأين؛ الجزء الحقيقي a، والجزء التخيّلي ib.
تستخدم الاعداد المركبة في الكثير من المجالات ولا سيما تلك المرتبطة بتوضيح وتمثيل الحركات الدورية كما هو الحال في التيار المتناوب والأمواج الضوئية، والأمواج المائية، وغيرها من المواضيع التي تُبنى على قيمة Sin (جيب الزاوية)، أو Cosine (تجيب أو جيب تمام الزاوية)، كما أنّ هناك مجموعةً من الصيغ الرياضية التي تعمل على حل المشكلات العلمية اعتمادًا على الأعداد المركبة هذه.
الأرقام الحقيقية هي جميع الأرقام الموجودة، سواء منها السالبة أو الموجبة، والكسرية أو الصحيحة، والجذر أو الصفر؛ فمثلًا نجد الأرقام 15، -30، 5/4، 0، جميعها أعداد حقيقية، أمّا الرقم الوهمي (التخيّلي) فهو عبارةٌ عن رقمٍ غير حقيقيٍّ، وهو الرقم الذي يكون ناتج رفعه للأس 2 (تربيعه) عددًا سالبًا مثل جذر العدد -4.[footnote]Complex Numbers in Maths، من موقع: byjus.com، اطّلع عليه بتاريخ February/16/2020 | 03:18 PM[/footnote]
واجه العلماء مشكلة الاعداد العقدية لأول مرة في عهد الأهرامات في القرن الأول الميلادي، عندما حاول هيرو السكندري (Heron of Alexandria) حساب حجم المخروط الناقص للهرم، الأمر الذي أوجب عليه حساب الجذر التربيعي لقيمةٍ سالبةٍ، وذلك في عام 75 للميلاد.
فيما أعلن عالم الرياضيات الهندي بهاسكارا أشاريا (Bhashara Acharya) عام 486 ميلادي أنّ مربع الرقم الموجب أو السالب هو رقم موجب، ولا يمكن أن يكون الجذر التربيعي رقمًا سالبًا، الأمر الذي أيده آخرون من العلماء، إلى أن قام الفيلسفوف والرياضي الإيطالي جيرولامو كاردانو (Girolamo Cardano) بإصدار كتابه (Ars Magna (The Great Art عام 1545 للميلاد، والذي عمل فيه على حل المعادلات التربيعية والتكعيبية، وكان إنجازًا مهمًّا بعد حوالي 3000 من قيام البابليين بحل المعادلات التربيعية، وقد تتضمن كتابه استخدام الجذر التربيعي لعددٍ سالبٍ بمعزلٍ عن كون النتيجة التي وصل إليها مبهمة إلى حدٍّ ما، إلّا أنّ ذلك فتح الباب لعلماء آخرين للبحث في هذا المجال.[footnote]History of Complex Numbers، من موقع: link.springer.com، اطّلع عليه بتاريخ February/16/2020 | 03:22 PM[/footnote]
العمليات على الاعداد المركبة
جمع الاعداد العقدية
عند جمع عددين عقديين نقوم بجمع الجزأين الحقيقين معًا، ثم جمع الجزأين الوهميين معًا كذلك الأمر، ويمكن التعبير عن ذلك بالعلاقة:
a + bi) + (c + di) = (a + c) + (b + d)i)
فمثلًا لجمع العددين العقديين 2+3i و 4+7i يكون:
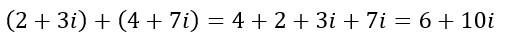
في حال كان العددان العقديان أو أحدهما يتضمن إشارةً سالبةً (عددًا سالبًا)، نقوم بمراعاة ذلك بدقّةٍ وجوبُا في عملية الجمع مثلًا:
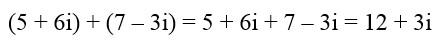
طرح الاعداد العقدية
لطرح عددين عقديين نتبع العلاقة التالية:
a + bi) – (c + di) = (a – c) + (b – d)i)
بمعنى آخر نقوم بضرب العامل السالب - (العدد -1 فعليًّا) بالعدد المطروح، ثم نكمل العملية وكأنّها عملية جمعٍ. مثلًا:
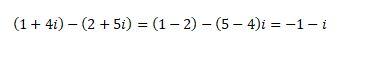
أو كان بإمكاننا تطبيق العلاقة بشكلٍ مباشرٍ.[footnote]Complex Number Formulas، من موقع: www.mathwords.com، اطّلع عليه بتاريخ February/16/2020 | 03:22 PM[/footnote]
ضرب الاعداد العقدية
لضرب عددين عقديين نقوم بفك الأقواس، وذلك من خلال ضرب كل جزءٍ من العدد العقدي الأول بكل جزءٍ من العدد العقدي الثاني، مع الأخذ بعين الاعتبار أنّ i2 = -1، ومن ثم نقوم بجمع الأجزاء المتشابهة عبر جمع الأجزاء الحقيقية معًا وجمع الأجزاء الوهمية معًا، وكمثال:[footnote]Multiplying Complex Numbers، من موقع: www.mesacc.edu، اطّلع عليه بتاريخ February/16/2020 | 03:22 PM[/footnote]
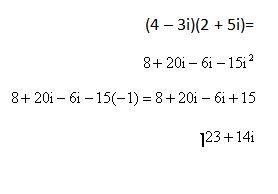
لضرب عددٍ حقيقيٍّ بعددٍ عقديٍّ، نقوم بضرب هذا العدد الحقيقي بكل جزءٍ من أجزاء العدد العقدي.[footnote]Multiplying complex numbers، من موقع: www.khanacademy.org، اطّلع عليه بتاريخ February/16/2020 | 03:22 PM[/footnote]
قسمة الاعداد المركبة
من المعلوم أنّه من غير الممكن التقسيم على عددٍ وهميٍّ، لذلك لا بدّ من إيجاد طريقةٍ ما تمكننا من التخلص من الجزء الوهمي الموجود في المقام ليتحول المقام إلى عددٍ حقيقيٍّ يمكن التقسيم عليه، لذلك نضرب المقام بمرافقه والذي يوجب علينا ضرب البسط بالمرافق نفسه أي لتقسيم (a + bi) على (c + di) يصبح:

ومن ثم نقوم بتوزيع البسط والمقام لتبسيط العملية؛ أي نجمع بين الأجزاء الحقيقية والأجزاء الوهمية في كلٍّ من البسط والمقام، مع الأخذ بعين التنبّه طبعًا إلى أنّ i2= -1، ومن ثم كتابة الناتج بصيغة a + ib بعد تبسيطها لأكبر درجة ممكنة ومثال على ذلك:[footnote]divide complex numbers، من موقع: www.mesacc.edu، اطّلع عليه بتاريخ February/16/2020 | 03:22 PM[/footnote]
