ما هي المصفوفة
تم التدقيق بواسطة: فريق أراجيك
المصفوفة كمصطلحٍ استخدمت في كثيرٍ من المجالات باختلاف الزمان والمكان، ففي روما القديمة كانت المصفوفة حيوانًا يحتفظ به للتربية، أو يطلق هذا المصطلح على النبات الأم الذي تستخدم بذوره لإنتاج أنواعٍ أخرى من النباتات. أمّا في اللغة الإنكليزية كان لهذه الكلمة الكثير من المعاني؛ فعلماء الرياضيات استخدموها لتنظيم مستطيلٍ من الأرقام أو الرموز التي تستخدم لإجراء حساباتٍ مختلفةٍ، أما علماء الجيولوجيا استخدموها للدلالة على التربة أو الصخور التي يتم اكتشاف أحافير فيها، وبشكلٍ عام كانت المصفوفة اختيارًا جيدًا كاسمٍ للواقع الذي يجد فيه جميع البشر أنفسهم يعيشون في سلسلةٍ من أفلام الخيال العلمي الشهيرة.
ابتكر اسم المصفوفة لأول مرةٍ سنة 1848 على يد جي جي سيلفستر كاسمٍ لمجموعةٍ مرتبةٍ من الأرقام، وفي 1855 قدم آرثر كايلي المصفوفة على أنها تمثيلٌ لعناصرٍ خطيةٍ، وهذه الفترة اعتبرت بداية الجبر الخطي ونظرية المصفوفات.
تعريف المصفوفة
هي مجموعةٌ من الأرقام مرتبةٌ في عددٍ من الصفوف والأعمدة، عادةً تكون هذه الأرقام حقيقيةً ويمكن أن تكون معقدةً.
كما يمكن تعريفها بشكلٍ عام بأنها دالة رياضية خطيّة تحول مجموعة بداية أي منطلقٍ، إلى مجموعة وصول أو نهاية (مستقر).
مجموعة المنطلق والمستقر يمكن أن تكون مكونةً من أعدادٍ صحيحةٍ أو عقدية أو أشعة من الأعداد، كما يمكن أن تكون هاتان المجموعتان مكونتان من دالاتٍ رياضيةٍ أو أشعة دالات رياضية، ونرمز للمصفوفة بقوسين مربعين كبيرين أو هلالين يُكتب ضمنها عناصر المصفوفة كما في الشكل:
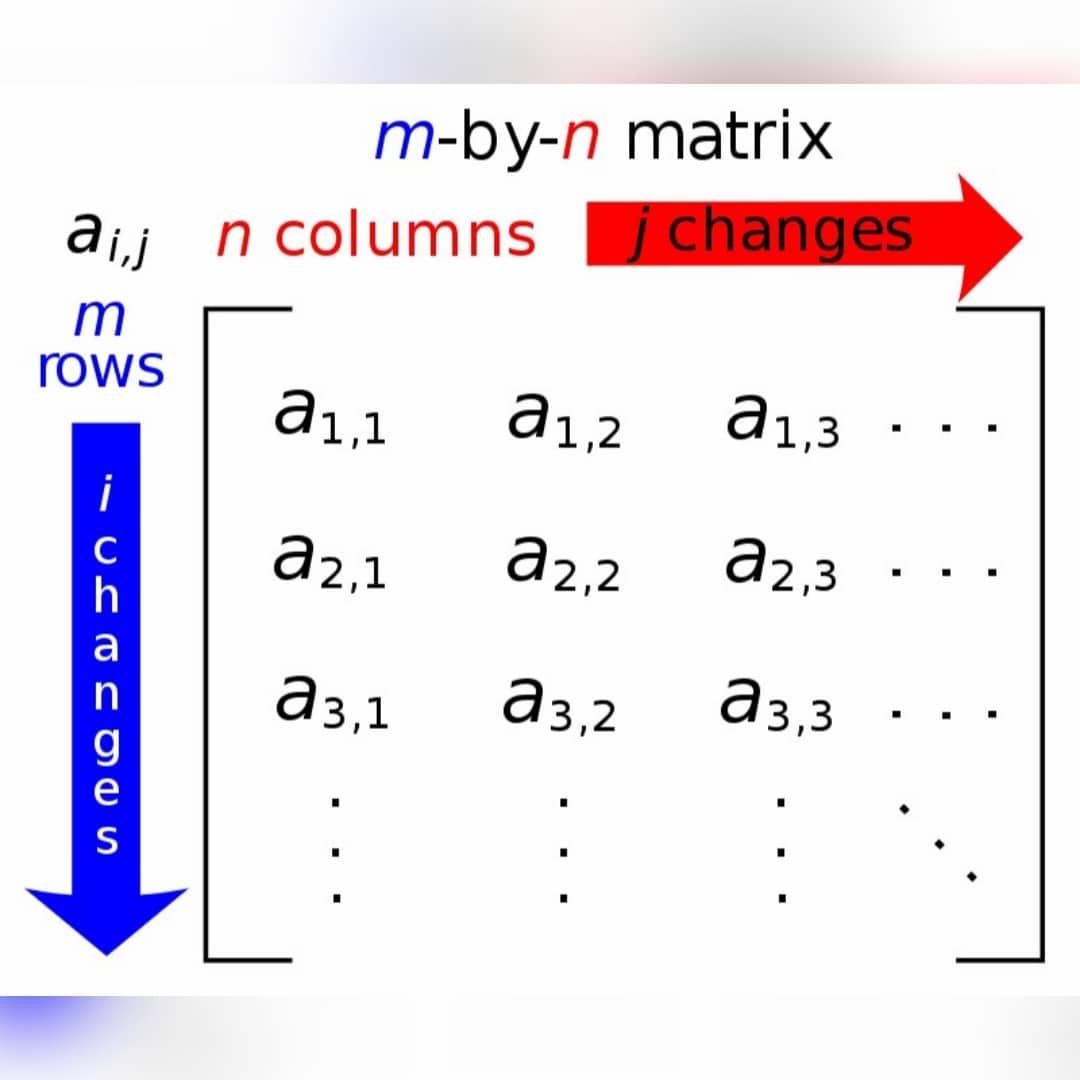
حيث aij أعداد صحيحة أو مركبة أو عقدية.
يُرمز للمصفوفة بحرفٍ لاتينيٍّ كبيرٍ وتحته عددين طبيعيين على شكل جداء هما m و n حيث m عدد أسطر المصفوفة و n عدد الأعمدة (مثال Am*n ).
تُدعى الخطوط الأفقية في المَصفوفة بالأسطر بينما تُدعى الخطوط العمودية بالأعمدة، أما الأعداد تُدعى مدخلات المصفوفة أو عناصرها حيث لكل عنصرٍ موقع محدد.
يدل عادةً على أي مدخلٍ في المَصفوفة بحرفٍ لاتينيٍّ صغيرٍ وأسفله رقمين صغيرين بحيث يُمثل العدد الأول رقم الصف والثاني رقم العمود ( مثلاً: العنصر في الزاوية العليا اليسرى هو عنصر من العمود الأول والصف الأول وهكذا …).
تعاريف خاصة بالمصفوفات
- حيّز المصفوفة أو رتبتها أو قياسها: يعرّف بأنه عدد الأسطر في جداء عدد الأعمدة؛ أي إذا كان لدينا مصفوفة تحتوي على 5 أسطر و 3 أعمدة فإن قياسها أو رتبتها هو 3*5 .
- المتّجه: هو المصفوفة المؤلفة من صفٍ واحدٍ وعمودٍ واحدٍ، حيث أن المصفوفة ذات العمود الواحد يُرمز لها بالشكل Am*1 وتعرف باسم متجه عمودي، بينما المصفوفة المؤلفة من صف واحد يُرمز لها ب A1*n وتعرف باسم متجه صفي.
- المصفوفة المربعة: هي مصفوفةٌ تحوي نفس العدد من الأسطر والأعمدة ويُرمز لها An*n كما في الشكل:
- المَصفوفة المنفردة: هي المصفوفة المربعة التي ليس لها نظيرٌ ضربيٌّ أما التي لها نظير ضربي تسمى غير منفردةٍ.
- المَصفوفة اللانهائية: هي المصفوفة التي تحوي على عددٍ لا حصر له من الصفوف أو الأعمدة أو كليهما.
- المَصفوفة الفارغة: هي مصفوفةٌ بدون صفوف ولا أعمدة وتستخدم في برامج الكمبيوتر .
- منقول مصفوفة: هو المَصفوفة الناتجة عن تبديل الأعمدة بالأسطر ويرمز لها AT ومن خواصها أن منقول مجموع مصفوفتين هو مجموع منقول مصفوفتين أي (A+B)T = AT+BT ، وأيضًا منقول حاصل ضرب مصفوفتين هو حاصل ضرب المصفوفتين بشكلٍ معاكسٍ لمنقولهما أي ( A.B)T = BT*AT
- معكوس مصفوفة: هو المعكوس الضربي للمصفوفة بحيث يكون حاصل ضرب المصفوفة في معكوسها يساوي مصفوفة الواحد أي B = In وتدعى المصفوفة B مقلوب A ورمزها A-1 .
العمليات على المصفوفات
تُجرى عمليتي الجمع والطرح على مصفوفتين بشرط أن يكون لهما نفس الرتبة، أي لهما نفس عدد الصفوف ونفس عدد الأعمدة وتتم العمليتان عنصرًا مع العنصر المقابل له.
لا تتم عملية ضرب مصفوفتين إلّا عندما يكون عدد أعمدة المصفوفة الأولى يساوي عدد صفوف الثانية مهما كانت رتبة المصفوفة، ولدى ضرب مصفوفة وحيدة العنصر بمصفوفةٍ متعددة العناصر يُضرب العنصر الوحيد مع كل عنصر من عناصر المصفوفة، والنتيجة مصفوفة لها العدد نفسه من العناصر، أما ضرب مصفوفة وحيدة السطر في مصفوفة وحيدة العمود هو مصفوفة وحيدة العنصر. ولعملية الضرب عدة خصائص إلا أنها ليست عمليةً تبديليةً أي A.B لا يساوي B.A.
أهمية المصفوفة
تُستخدم المصفوفات وتطبيقاتها في معظم المجالات العلمية، في كل فرعٍ من فروع الفيزياء مثل الميكانيكية والبصريات الهندسية والكهرومغناطيسية وميكانيك الكم ولدراسة الظواهر الفيزيائية مثل حركة الأجسام الصلبة وأيضًا في رسومات الكمبيوتر ومعالجة النماذج الثلاثية الأبعاد وعرضها على شاشةٍ ثنائية الأبعاد، كما تستخدم في نظريات الاحتمالات والإحصاء، وفي الاقتصاد تستخدم لوصف أنظمة العلاقات الاقتصادية.
 ASUS
ASUS TV
TV Partner With Us
Partner With Us