ما هو التكامل

حساب التفاضل والتكامل هو أحد فروع الرياضيات الذي يتعامل مع معدلات التغير والحركة، وقد نشأ هذا العلم انطلاقًا من الرغبة في فهم الظواهر الفيزيائية المختلفة مثل مدارات الكواكب وآثار الجاذبية.

أدى نجاح حساب التفاضل والتكامل في صياغة القوانين الفيزيائية والتنبؤ بنتائجها إلى تطوير قسمٍ جديدٍ في الرياضيات يسمى التحليل، والذي يعتبر حساب التفاضل والتكامل جزءًا كبيرًا منه.

يعتبر حساب التفاضل والتكامل اليوم اللغة الأساسية للعلوم والهندسة، والوسيلة الأساسية التي يتم التعبير بها عن القوانين الفيزيائية بمصطلحاتٍ رياضية، ويعتبر أداةً علميةً لا تقدر بثمنٍ في التحليل الإضافي للقوانين الفيزيائية، وفي التنبؤ بسلوك النظم الكهربائية والميكانيكية التي تحكمها هذه القوانين، وفي اكتشاف قوانين جديدة.

غالبًا ما يُعزى اكتشاف حساب التفاضل والتكامل إلى عالمين اثنين؛ هما إسحق نيوتن، وجوتفريد لايبنيز اللذان مهدا لأساسات هذا العلم بشكلٍ مستقلٍ. على الرغم من أنه قد كان لكليهما دورٌ جوهريٌّ في إنشائه، إلا أنهما فكرا في المفاهيم الأساسية بطرقٍ مختلفةٍ للغاية؛ فمن جهةٍ اعتبر نيوتن المتغيرات تتغير مع مرور الوقت، بينما فكر لايبنز في المتغيرات x وy على أنها تتراوح عبر متتالياتٍ غير متناهيةٍ من القيم المتقاربة، وقدم رمزَي dx و dy كاختلافاتٍ بين القيم المتعاقبة لهذه المتتاليات.

علم ليبنيز أن dy / dx يعطي الظل، ولكن لم يستخدمه كخاصيةٍ محددةٍ. استخدم نيوتن من ناحيةٍ أخرى لحساب الظل قيم x و y التي كانت عبارة عن سرعاتٍ محدودةٍ. بالطبع لم يفكر لايبنيز ولا نيوتن فيما يتعلق بالدوال، ولكن كلاهما كان يفكّر دائمًا في الرسوم البيانية، وبالنسبة لنيوتن كان حساب التفاضل والتكامل هندسيًا، بينما توجه لايبنيز باتجاه التحليل.

من المثير للاهتمام أن نلاحظ أن ليبنيز كان مدركًا جدًا لأهمية الترميز الجيد والتفكير في الرموز التي استخدمها، ونيوتن من ناحيةٍ أخرى كان يرمز ويكتب لنفسه أكثر من أي شخصٍ آخر. وبالتالي فقد كان يميل إلى استخدام أي ترميزٍ يتبادر إلى ذهنه في ذلك اليوم، وتبين أن هذا كان ذا أهمية في التطورات اللاحقة. كان تدوين لايبنز أكثر ملاءمة لتعميم حساب التفاضل والتكامل على متغيراتٍ متعددةٍ، ونتيجةً لذلك فإن الكثير من الرموز المستخدمة في حساب التفاضل والتكامل اليوم ترجع إلى لايبنز.

الاستخدام الأساسي للتكامل هو على شكل نسخة مستمرة من عملية الجمع، لكن يتم حساب التكاملات في كثيرٍ من الأحيان عن طريق عرض التكامل باعتباره في الأساس عملية عكسية للتفاضل. (هذا ما يسمى في الحقيقة النظرية الأساسية لحساب التفاضل والتكامل)

التدوين الخاص بالتكامل الذي تمسكنا به لأسبابٍ تاريخيةٍ هو بنفس غرابة التدوين الخاص بالمشتقات، ويكتب تكامل الدالة fx بالنسبة للمتغير x على الشكل التالي:

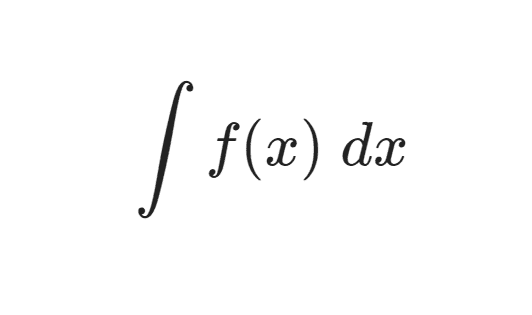
يمكن ملاحظة أن التكامل (تقريبًا) هو معكوسٌ لعملية التفاضل:

إن الثابت C الإضافي والذي يُطلق عليه ثابت التكامل يملك هدفًا مهمًا حقًا، لأنه بعد كل عملية تفاضلٍ تتم تنحية الثوابت، وهذا هو السبب في أن التكامل والتفاضل ليسا عمليتين عكسيتين تمامًا لبعضهما البعض.