الأعداد الأولية.. ما هي وكيف أعرف إن كان العدد أوليًا أم لا؟

تم التدقيق بواسطة: فريق أراجيك
الأعداد الأولية هي أعداد لا تقبل القسمة إلا على نفسها وعلى الواحد، وهي أساس علم الرياضيات.
يمكن تحديد الأعداد الأولية باستخدام التحليل إلى عوامل أو القسمة بواسطة الآلة الحاسبة.
تُستخدم الأعداد الأولية في التشفير، وأبرز تطبيقاتها هو نظام RSA.
تعتبر الأعداد الأولية واحدة من أهم المفاهيم الأساسية في علم الرياضيات والأرقام، فهي تلعب دورًا بارزًا في عدة مجالات مختلفة، بما في ذلك التشفير والأمن السيبراني وحتى دراسة الأنماط العددية، يتناول هذا المقال في هذا المقال تعريف مفهوم تلك الأعداد وخصائصها وأهم تطبيقاتها في العصر الحديث.
ماذا نقصد بالأعداد الأولية؟
تُعرف الأعداد الأولية بأنّها أي أعداد صحيحة تحقق شرطين أساسيين، أكبر من الواحد ولا تقبل القسمة إلا على نفسها وعلى العدد واحد، أما الأعداد التي تقبل القسمة على أعداد أخرى بخلاف نفسها والواحد، فتُعرف بالأعداد المركبة، حيث يُعرَّف العدد المركب بأنه أي عدد أكبر من الواحد وله قواسم إضافية غير الواحد ونفسه.
فيما يخص العدد واحد، فهو لا يُصنَّف كعدد أولي ولا كعدد مركب، وكذلك الرقم صفر، وباستثناء هذين العددين، فإن كل رقم أكبر من الواحد يكون إما عددًا أوليًا أو عددًا مركبًا. [footnote]، Prime Numbers - Facts, Examples, & Table Of All Up To 1,000، من موقع: www.factmonster.com، اطّلع عليه بتاريخ 27-10-2019.[/footnote]
تُعتبر هذه الأعداد أساس علم الأعداد، حيث تلعب دور أساسي في مختلف فروع الرياضيات والتطبيقات الحاسوبية، ومن بين الأعداد الأولية الأولى في سلسلة الأرقام نجد: 2، 3، 5، 7، 11، 13، 17، 19، 23، 29. [footnote]، prime number، من موقع: whatis.techtarget.com، اطّلع عليه بتاريخ 27-10-2019.[/footnote]
كيفية معرفة الاعداد الاولية
هناك طريقتان أساسيتان يمكن من خلالهما تحديد ما إذا كان العدد أوليًا:
- التحليل إلى عوامل:
تعتمد هذه الطريقة على تحليل العدد إلى عوامله الأولية، على سبيل المثال، العوامل الأولية للعدد هي 1 و10 لكن له عوامل أخرى هي 2 و5، لأن حاصل ضربهما هو 10 وهما غير أوليين، لذا يُعد العدد 10 عددًا مركبًا.
- باستخدام الآلة الحاسبة:
يمكن استخدام العمليات الحسابية والقسمة لاختبار أولية عدد معين، على سبيل المثال، لمعرفة ما إذا كان العدد 57 عددًا أوليًا، يمكن قسمته على 2، فنجد أن الناتج 27.5، وهو عدد ليس صحيحًا، مما يعني أن 57 ليس من مضاعفات 2، لكن عند قسمته على 3، نجد أن الناتج هو 19، وهو عدد صحيح، ما يثبت أن 57 يقبل القسمة على 3، وبالتالي فهو ليس عددًا أوليًا. [footnote]، Determining If a Number Is Prime، من موقع: www.thoughtco.com، اطّلع عليه بتاريخ 27-10-2019.[/footnote]
ما هو تاريخ الأعداد الأولية؟
عُرف أول عدد أولي منذ العصور القديمة حين قام عالما الرياضيات اليونانيان إقليدس (fl.c.300) قبل الميلاد وإراتوسيتنس (c.276-194) قبل الميلاد بدراستها، وقد أعطى إقليدس أول دليل له على وجود أعداد أولية لا حصر لها، وهناك نتيجتان شهيرتان تتعلقان بتوزيع الأعداد الأولية وتستحقان الذكر هما: نظرية الأعداد الأولية، ودالة زيتا ريمان.
ساعد ظهور الحواسيب والتكنولوجيا في اكتشاف أعداد أولية بملايين الأرقام، وقد كان الاعتقاد السائد أنّ تلك الأرقام لن يكون لها أي تطبيقٍ ممكنٍ، إلا أنّها استخدمت فيم بعد في صناعة شيفراتٍ غير قابلة للكسر ساعدت في جعل مجتمعنا الرقمي الحالي أكثر أمان وحماية. [footnote]، Prime، من موقع: www.britannica.com، اطّلع عليه بتاريخ 27-10-2019.[/footnote]
ما أهمية الأعداد الأولية في التشفير؟
تُستخدم الأعداد الأولية على نطاق واسع في مجال التشفير، وأبرز مثال على ذلك هو نظام التشفير RSA، إذ يعتمد هذا النظام على اختيار عددين أوليين كبيرين وحسابهما معًا لإنشاء مفتاح تشفير آمن، كلما زاد حجم الأعداد الأولية، زادت صعوبة كسر التشفير.
إذا أراد شخصان تبادل المعلومات المشفرة عبر الإنترنت، فإن أحدهما يمكنه اختيار عددين أوليين كبيرين وحسابهما، ثم مشاركة الناتج علنًا، نظرًا لأن تحليل العدد الكبير إلى عوامله الأولية يتطلب وقتًا طويلًا جدًا حتى باستخدام أقوى الحواسيب، يبقى التشفير آمنًا، مما يجعل RSA من أكثر الأنظمة أمانًا حتى اليوم.[footnote]، HOW PRIME NUMBERS ARE USED FOR CYBERSECURITY، من موقع: psmag.com، اطّلع عليه بتاريخ 27-10-2019.[/footnote]
ما هي الأعداد الأولية حتى 1000؟
للباحثين والدارسين الذين يحتاجون إلى قائمة بالأعداد الأولية، نقدم فيما يلي جدولًا يحتوي على جميع الأعداد الأولية من 1 إلى 100:
| 5 | 3 | 2 |
| 13 | 11 | 7 |
| 23 | 19 | 17 |
| 37 | 31 | 29 |
| 47 | 43 | 41 |
| 61 | 59 | 53 |
| 73 | 71 | 67 |
| 89 | 83 | 79 |
| 97 |
كما يقدم الجدول التالي الأعداد الأولية حتى 1000:
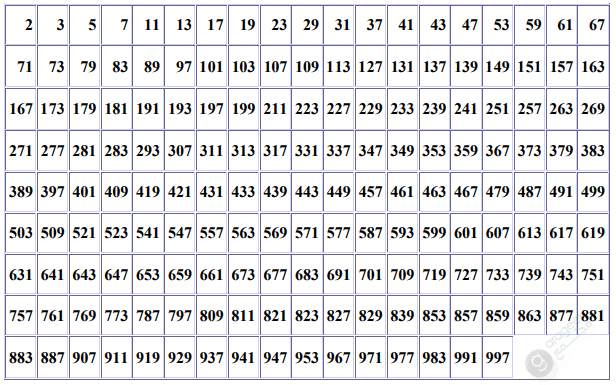
يتوفر الجدول بصيغة PDF للتحميل والاستخدام في الدراسات الرياضية.
أهم الأسئلة الشائعة حول الأعداد الأولية
جاءت التسمية من كونها تُشكِّل الأساس لجميع الأعداد الأخرى، حيث يمكن تكوين أي عدد صحيح من خلال ضرب الأعداد الأولية.
هناك بعض القواعد الأساسية لتحديد أولية الأعداد الكبيرة:
إذا كان العدد ينتهي بأحد الأرقام 0، 2، 4، 6، 8، فهو ليس عددًا أوليًا.
جمع أرقام العدد: إذا كان المجموع قابلاً للقسمة على 3، فالعدد ليس أوليًا.
إذا لم ينطبق الشرطان السابقان، يتم حساب الجذر التربيعي للعدد، ومن ثمّ يتم اختبار قابلية قسمة العدد على جميع الأعداد الأقل من جذره التربيعي، إذا كان العدد يقبل القسمة على أي من هذه الأعداد، فهو عدد غير أولي، وإلا فهو أولي.
لا، العدد 1 ليس عددًا أوليًا، حيث إن الأعداد الأولية يجب أن يكون لها عاملان فقط، والعدد 1 له عامل واحد فقط.
ختامًا، إن الأعداد الأولية ليست مجرد أرقام رياضية، بل هي عنصر أساسي في علوم الحوسبة والأمان الرقمي، مع التطور التكنولوجي يظل البحث في الأعداد الأولية مجالًا خصبًا للابتكار والتطوير في التشفير وحماية البيانات.
 TV
TV Partner With Us
Partner With Us