ما هي الجمل المثلثية
تم التدقيق بواسطة: فريق أراجيك
الجمل المثلثية أو الدوال المثلثية هي عبارةٌ عن دوال أولية بالنسبة للزاوية تحدد العلاقة بين زوايا المثلث وأضلاعه، وتتكون من ست دوال رئيسية هي جيب الزاوية Sin، وجيب تمام الزاوية Cos، وظل الزاوية Tan، وظل تمام الزاوية Ctan، وقاطع الزاوية Sec، وقاطع تمام الزاوية Csc، ولكل دالةٍ من الدوال السابقة دالة معكوسة.
تستخدم تلك الدوال في دراسات الرياضيات بالأخص في حل المعادلات التفاضلية وفي التحليل الرياضي، وتسهل تطبيق علم المثلثات في مسائل الاستقصاء والهندسة والملاحة.[footnote]، Trigonometric function، من موقع: www.britannica.com، اطّلع عليه بتاريخ 11/11/2019[/footnote]
التعبير عن الجمل المثلثية
كل دالةٍ من الدوال هي عبارةٌ عن نسبة ضلعين من المثلث بالنسبة لأحد الزوايا، والفرق الوحيد بين الدوال الست هو زوج الأضلاع الذي نستخدمه، للتعبير عن الدوال نحتاج إلى مثلثٍ بحيث:
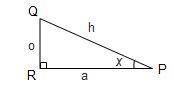
- x: يعبر عن الزاوية المستخدمة في التعبير عن الدوال.
- a: يعبر عن طول الضلع المجاور للزاوية (x).
- o: يعبر عن طول الضلع المقابل للزاوية (x).
- h: يعبر عن طول الوتر.
يكون لدينا:
- Sin (x) = o/h
- Cos (x) = a/h
- tan (x) = o/a
- Cot (x) = a/0
- Sec (x) = h/a
- Csc (x) = h/o
لكل دالةٍ من الدوال الست السابقة دالة عكسية عملها معاكس للدالة المقابلة لها، ويعبر عنها بإضافة الأحرف ARC أمام الدالة الموازية لها أو برفع الدالة الموازية لها للأس -1؛ فعلى سبيل المثال، إنّ معكوس دالة الـ COS هو ArcCos أو cos-1.
تستخدم دالة الـ COS للحصول على جيب تمام الزاوية، بينما تستخدم دالتها المعكوسة ArcCos للحصول على الزاوية التي تقابل قيمة جيب التمام.[footnote]، Trigonometry functions - introduction، من موقع: www.mathopenref.com، اطّلع عليه بتاريخ 11/11/2019[/footnote]
مثال نظري
تستخدم الجمل المثلثية في الكثير من التطبيقات العملية في عمليات المسح والبناء والهندسة وحتى الطب، فعلى سبيل المثال ليكن لدينا طائرة تقلع على مدرج الطيران بزاوية 23 درجة كم ستكون المسافة التي قطعتها عندما يصل ارتفاعها إلى 2500 متر؟
لحل المثال السابق نرسم مثلثًا بالشكل التالي، وستكون المسافة المراد حسابها عبارةً عن طول وتر المثلث.
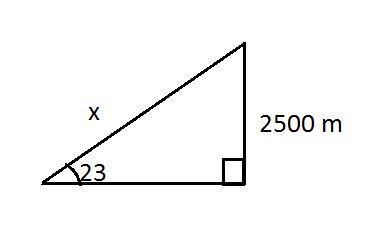
بما أننا نعلم طول الضلع المجاور
للزاوية فيمكننا حساب طول الوتر باستخدام دالة الجيب فيكون لدينا:
Sin (23) = 2500 / x
ومنه
نستنتج:
X= 2500 / sin (23) = 6398.3 m
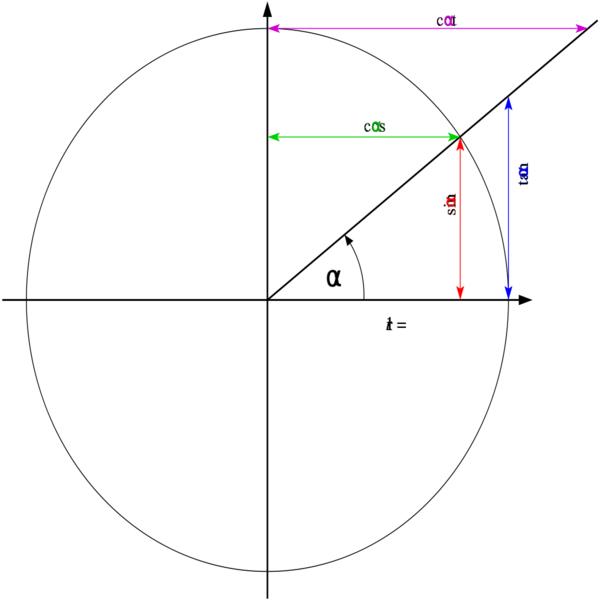
دائرة الوحدة
يمكن التعبير عن الجمل المثلثية باستخدام دائرة الوحدة التي تمثل أحد أكثر الأدوات المساعدة في حسابات الدوال المثلثية، حيث يحتوي الربع الأول من الدائرة على جميع الزوايا القياسية.
الطريقة التي يتم فيها استخدام دائرة الوحدة هي عن طريق رسم خطٍ من مركز الدائرة باتجاه الخارج بحيث يتوافق مع زاويةٍ معينةٍ، تعبر إحداثيات النقطة التي يتقاطع فيها الخط مع الدائرة (x,y) جيب الزاوية وجيل التمام لها حيث x هو جيب تمام تلك الزاوية و y هو جيب تلك الزاوية

- أي من الدائرة السابقة يمكننا ملاحظة أن:
- 2 / 3 √ = (6/Cos (π
- وكذلك:
- 2 / 1 = (6/Sin (π
كما يجب الانتباه إلى أنه عند الدوران عكس اتجاه دوران عقارب الساعة تكون الزوايا موجبةً لكن عند الدوران في اتجاه عقارب الساعة تكون الزوايا سالبةً وأن الدورة الكاملة هي عبارةٌ عن 2π بالتالي المحور xيتوافق مع الزوايا 0 و 2π و 4π و 2π- و 4π- حسب جهة الدوران.[footnote]، Trig Functions، من موقع: tutorial.math.lamar.edu، اطّلع عليه بتاريخ 11/11/2019[/footnote]
متطابقات الجمل المثلثية
عند اشتقاق الجمل المثلثية الأساسية ينتج لدينا العديد من المتطابقات التي يمكن استخدامها في حل العديد من المسائل والتطبيقات وهي:
- المتطابقات العكسية:
- (Sin (A) = 1 / Cos (A
- (Cos (A) = 1 / Sin (A
- (tan (A) = 1 / Cot (A
- (Cot (A) = 1 / tan (A
- (Sec (A) = 1 / Cos (A
- (Csc (A) = 1 / Sin (A
- المتطابقات النسبية:
- (tan (A) = Sin (A) / Cos (A
- (Cot (A) = Cos (A) / Sin (A
- متطابقات فيثاغورث الهندسية:
- sin2 (A) + cos2 (A) = 1
- (1 + tan2 (A) = Sec2 (A
- (1 + Cot2 (A) = Csc2 (A
- متطابقات الجمع والطرح:
- (Sin (A + B) = Sin (A) Cos (B) + Sin (B) Cos (A
- (Sin (A - B) = Sin (A) Cos (B) - Sin (B) Cos (A
- (Cos (A + B) = Cos (A) Cos (B) - Sin (A) Sin (B
- (Cos (A - B) = Cos (A) Cos (B) + Sin (A) Sin (B
- ((tan (A + B) = ( tan(A) + tan (B) ) / (1 – tan (A)tan(B
- ( (tan (A + B) = (tan (A) - tan (B ) ) / (1 – tan (A) tan(B
- متطابقات ضعف الزاوية:
- (Sin (2A) = 2 Sin (A) Cos (A
- (Cos (2A) = Cos2 (A) – Sin2 (A) = 2 Cos2 (A) – 1 = 1 – Sin2 (Ac
- [footnote]، Trigonometry (trig) identities، من موقع: www.mathopenref.com، اطّلع عليه بتاريخ 11/11/2019[/footnote] ((tan (2A) = (2 tan (A)) / (1 – tan2 (A
