ما هي متتالية فيبوناتشي
تم التدقيق بواسطة: فريق أراجيك
يحتوي علم الرياضيات على العديد من النظريات والمتتاليات التي يتم بناء الكثير من الحلول المعقدة عليها، ويتوقف فهم هذه الأشياء على طرق العرض والأساليب البسيطة، سنتكلم اليوم على أحد أهم متتاليات الرياضيات، وهي متتالية فيبوناتشي.
في هذه المتتالية يكون كل رقمٍ فيها عبارةً عن مجموع الرقمين السابقين له في المتتالية، لذلك تكون المتتالية على هذا النحو: 0، 1، 1، 2، 3، 5، 8، 13، 21، ... وهكذا، وتكون المعادلة الرياضية التي تصف هذه المتتالية هي: Xn+2=Xn+1+Xn
أهمية متتالية فيبوناتشي
تعرف هذه المتتالية بـ "رمز سر الطبيعة"، أو "قاعدة الطبيعة العالمية"، وذلك لأنها تعتبر من أهم الركائز التي يرتكز عليها مناهج الرياضيات في فصول المدارس الثانوية والجامعات. يقال أن متتالية فيبوناتشي تحكم أبعادها أساس كل شيءٍ، بدءًا من الهرم الأكبر في الجيزة، ووصولًا للغلاف المتوقع لكتب الرياضيات في المستقبل.[footnote]، What Is the Fibonacci Sequence?، من موقع: www.livescience.com، اطّلع عليه بتاريخ 12-12-2019[/footnote]
تكمن أهمية هذه المتتالية فيما تسمى بـ "النسبة الذهبية"، وهي قيمةٌ قدرها (1.618)، أو معكوسها وهو (0.618)، وسر أهمية هذه القيمة في أن كل رقمٍ في متتالية فيبوناتشي يزيد عن ما يسبقه في المتتالية بمقدار 1.618 ضعف، كما أن أي رقمٍ في المتتالية هو 0.618 ضعف الرقم الذي يليه، وتسمى هذه النسبة بالنسبة الذهبية لأنها تصف كل شيءٍ في الطبيعة، بدايةً من عدد الأوردة الموجودة في الألياف، إلى الرنين المغناطيسي في دوران بللورات الكوبالت.
استخدامات متتالية فيبوناتشي
تم اختراع هذه المتتالية عن طريق عالم الرياضيات الإيطالي «فيبوناتشي» في القرن الثالث عشر. سوف تنقسم متتالية فيبوناتشي إلى نسبٍ يعتقد البعض أنها سوف تتنبأ بأحوال السوق المالي.[footnote]، Fibonacci Numbers and Lines Definition and Uses، من موقع: www.investopedia.com، اطّلع عليه بتاريخ 12-12-2019[/footnote]
بينما تنطلق مزايا متتالية فيبوناتشي بشكلٍ كبيرٍ في نطاق الطبيعة بأكملها، لكن هناك جزء تظهر فيه أهمية المتتالية بشكلٍ كبيرٍ، وهو إمكانية التنبؤ بأسعار أسهم البورصة من خلالها. نظام الاستثمار الأشهر الذي يعتمد على متتالية فيبوناتشي هو نظرية موجة إليوت (Elliot wave)، ولكن هذه النظرية الكبيرة لم يتم استخدامها نظرًا لتعقيد بعض الأمور المرتبطة بها، وفي المقابل تم استخدام ثلاثة تطبيقاتٍ أخريات معتمدة على متتالية فيبوناتشي، هذه التطبيقات عملت على تفسير هبوط أسعار أسهم بعض الشركات، كما فسرت التغيرات المفاجئة في اتجاهات الأسهم، وتوقع اتجاهات الأسعار.[footnote]، 3 Important Uses of Fibonacci Numbers، من موقع: www.stocktrader.com، اطّلع عليه بتاريخ 12-12-2019[/footnote]
وجودها في الطبيعة
تتمثل هذه المتتالية في الطبيعة بطرقٍ مختلفةٍ، فهي تعكس بعض الأنماط التي تحدث بشكلٍ طبيعيٍّ، حيث يمكنك اكتشاف هذه الأشياء عن طريق دراسة الطريقة التي تنمو بها النباتات المختلفة، وإليك بعض الأمثلة التي توضح الأمر في النباتات:
- انظر إلى مجموعة البذور في مركز زهرة عباد الشمس، سوف تلاحظ الأنماط الحلزونية التي تنحني يمينًا ويسارًا. المثير للدهشة هنا، هو أنك إذا قمت بعدِّ هذه الأنماط الحلزونية سوف يكون الناتج هو رقم فيبوناتشي! وإذا قمت بتقسيم هذه الأشكال واحدة لليمين، وأخرى لليسار، سوف تحصل على رقمين من متتالية فيبوناتشي.

- تظهر متتالية فيبوناتشِي في الزهور وفروع النباتات: تمثل بعض النباتات متتالية فيبوناتشي في نقاط النمو الخاصة بها، وهي الأماكن التي تتكون منها فروع الأشجار. ينمو الجذع حتى ينتج فرع فنحصل على نقطتي نمو، ثم ينتج الجذع الرئيسي فرعًا آخر، فنحصل بذلك على مجمل ثلاث نقاط نمو، ثم ينتج الجذع والفرع الأول نقطتي نمو، فتكون المحصلة خمس نقاط نمو، وإذا نظرنا إلى تتابع عدد النقاط سوف نجده: (2، 3، 5)، وهو تتابع يعبر عن متتالية فيبوناتشي.
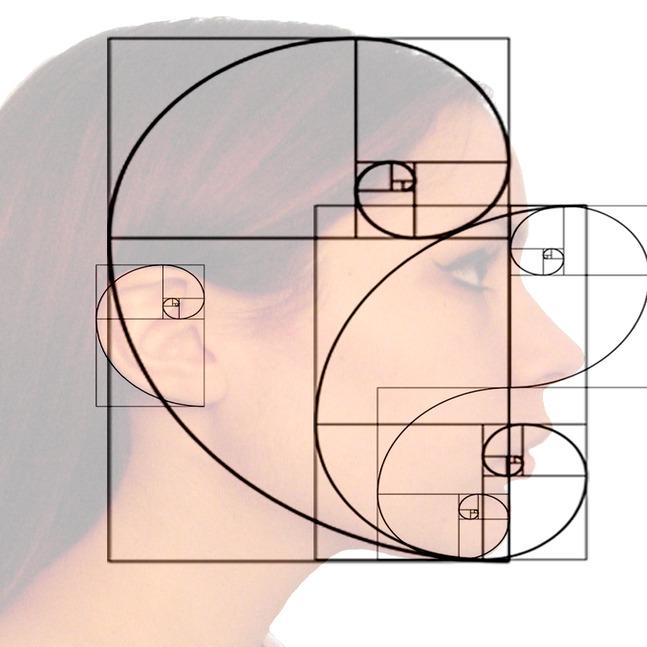
- تظهر هذه المتتالية في جسم الإنسان: إذا قمت بالوقوف أمام المرآة، وأمعنت النظر في نفسك، سوف تجد أن متتالية فيبوناتشي تظهر في جسمك، حيث أن أغلب أجزاء جسمك تتبع التتابع (1، 2، 3، 5)، فأنت لديك أنف واحد وعينان، وثلاث قطاعات في كل طرف من أطرافه (قطاع عند الإبط وقطاع عند الكوع وقطاع عند الرسغ)، كما لديك خمس أصابع في كل يد.
بعد أن استعرضنا هذه الأمثلة التي توضح ظهور هذه المتتالية في الطبيعة، يبقى السؤال: لما تنعكس هذه المتتالية على كل هذه الأنماط الطبيعية؟
لقد فكر العلماء في إجابة هذا السؤال لعدة قرونٍ. في بعض الحالات في الطبيعة، نجد أن العلاقة يمكن أن تكون محض صدفةٍ، وفي حالاتٍ أخرى، نجد أن النسبة هذه قد تم اختيارها دونًا عن غيرها لأنها أكثر فعاليةً، كالنمو في النباتات مثلًا.[footnote]، How are Fibonacci numbers expressed in nature?، من موقع: science.howstuffworks.com، اطّلع عليه بتاريخ 12-12-2019[/footnote]
 TV
TV Partner With Us
Partner With Us