الدوال الاسية

تم التدقيق بواسطة: فريق أراجيك
يتعامل الطلاب خلال مراحل دراستهم لمادة الرياضيات مع عددٍ مختلفٍ ومتنوعٍ من الدوال المعادلات الرياضية وطرق حلها للاستفادة منها في مختلف المجالات مستقبلًا، خاصةً ما يتعلق بالفيزياء والكيمياء والإحصاء وغيرها. فلنتعرّف هنا إلى الدوال الاسية (Exponential Functions).
تعريف الدوال الاسية
هي واحدةٌ من أكثر الدوال أهميةً في الرياضيات. تُستخدم للدلالة على علاقةٍ يتغير وفقها متغيرٌ مستقلٌ بطريقةٍ ثابتةٍ، كما التغير النسبي للمتغير التابع، وغالبًا ما تُكتب exp(x)، ويعتمد عليها في الفيزياء والكيمياء والهندسة والبيولوجيا الرياضية والاقتصاد والرياضيات. تتميز الدوال الاسية عن بقية الدوال بوجود الأس أو القوة (Exponents)؛ وهي المتغير ذاته، وهذا ما يخالف بقية الدوال، حيث يكون المتغير هو الأساس والقوة هي رقمًا.
بينما في الدالة الأسية، يتغير الوضع فيصبح المتغير هو القوة (الأس)، والأساس هو رقم وفق النموذج:

للتعامل مع الدوال الاسية لا بدّ من معرفة كيفية عملها، فإن كان الأس سالبًا يجب نقل الأساس إلى الجهة الأخرى من خط الكسر؛ أي بمعنى إن كانت قيمة المتغير x سالبة مثلًا (-1) تصبح الدالة الأسية التي تكون قيمة b=2:
بينما إن كانت قيمته موجبةً مثلًا 2 تصبح الدالة الأسية:[footnote]، Exponential Functions: Introduction، من موقع: www.purplemath.com، اطّلع عليه بتاريخ 8/1/2020[/footnote]
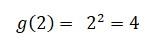
استخدام الدوال الاسية
يمكن استخدام الدوال الاسية في مجالاتٍ كثيرةٍ كحساب الفائدة المركبة في التعاملات المالية، ومعادلات النمو السكاني، والاضمحلال الإشعاعي، وهنا لا بدّ من الإشارة إلى أنه ليس بالضرورة أن تكون كافة الدوال الاسية المستخدمة مطابقةً للنموذج:
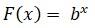
حيث يمكن تعديلها من خلال إضافة أو مضاعفة الثوابت، فمثلًا لنأخذ الدالة الأسية للفائدة المركبة والموافقة للنمط:
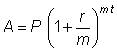
- P: الأساس ويدل على الاستثمارات الأولية التي تحسب فائدتها.
- A: الأموال المجموعة والتي تعطى عليها الفائدة.
- t: عدد السنوات التي سيحسب فيها الفائدة.
- r: نسبة الفائدة السوية.
- m: الفترات الزمنية لحساب الفائدة من كل عامٍ.
بالتالي يكون الأساس متمثلًا بالصيغة:
والأس mt والذي يمكن عند الحصول على قيم كل متغيرٍ من المتغيرات السابقة؛ الحصول على دالة أسية تشير إلى منحني تزايد الفائدة.[footnote]، Introduction to Exponential Functions ، من موقع: www.montereyinstitute.org، اطّلع عليه بتاريخ 8/1/2020[/footnote]
دالة النمو الأسي (Exponential Growth)
هي دالةٌ تشير إلى قيمٍ متزايدةٍ تبدأ بشكلٍ بطيءٍ ثم تزداد بوتيرةٍ متسارعةٍ مع مرور الوقت وهذا ما يدعى بالنمو، حيث تعبر عن معدل النمو المتزايد للسكان والعائدات أو استخدام تقنيةٍ ما بشكلٍ ثابتٍ. يمكن التعبير ع النمو الأسي لأيّ مجالٍ كان من خلال علاقةٍ بين المتغير x ومعدل النمو r والأس t الدال على الزمن مثلًا وفق الصيغة

حيث يتزايد معدل النمو (r)، كلما ازداد المتغير x ومع مرور الوقت (t). وهنا يمكن ملاحظة أن النمو الأسي أكبر وأسرع من النمو كثير الحدود.[footnote]، What Exponential Growth Really Looks Like (And How to Hit It)، من موقع: amplitude.com، اطّلع عليه بتاريخ 8/1/2020[/footnote]
دالة التناقص الأسي (Exponential Decrease)
هي إحدى الدوال الاسية المستخدمة في الرياضيات للدلالة على تناقص مقدارٍ معينٍ بمعدلٍ ثابتٍ خلال فترةٍ زمنيةٍ، ويمكن التعبير عنها بالصيغة:
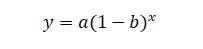
- Y: الكمية النهائية.
- a: الكمية الأساسية.
- b: عامل التناقص.
- x: الفترة الزمنية.
يختلف التناقص الخطي في اعتماد عامل التناقص على نسبة الكمية الحقيقية التي سيتغير الرقم الحقيقي الدال عليها مع مرور الوقت، في حين يتناقص الرقم الحقيقي بنفس المقدار خلال فترةٍ زمنيةٍ محددةٍ في الدالة الخطية. تستخدم دالة التناقص الأسي في العديد من المجالات العملية مثل حساب تكلفة استخدام شيءٍ محددٍ خلال فترةٍ زمنيةٍ طويلةٍ.[footnote]، Exponential Function and Decay، من موقع: www.thoughtco.com، اطّلع عليه بتاريخ 8/1/2020[/footnote]
الرسم البياني للدوال الأسية
عند دراسة الدوال الاسية من المفيد جدًا معرفة الشكل العام لرسمها البياني، حيث يوجد لذلك خياران؛ الأول حين يكون الأساس أكبر من 1، والثاني أصغر من 1.
الأساس في الدوال الاسية أكبر من 1
في حال كان الأساس أكبر من 1، سيزداد طول الرسم
البياني للدالة الأسية
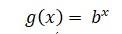
كلما اتجه إلى اليمين ويصبح أقصر كلما اتجه إلى اليسار ويقترب من المحور x دون أن يلامسه.
الأساس في الدوال الاسية أصغر من 1
في حال كان الأساس في الدالة الأسية أصغر من 1 لكنه موجبٌ، سيتجه الرسم البياني للدلالة إلى الأسفل، كلما اتجه إلى اليمين، لكنه يبقى موجبًا بينما سيزداد طوله بسرعةٍ كلما اتجه إلى اليسار. [footnote]، Exponential Functions ، من موقع: www.math.utah.edu، اطّلع عليه بتاريخ 8/1/2020[/footnote]
