كيف يتم حل المعادلات المثلثية
تم التدقيق بواسطة: فريق أراجيك
يتعامل الطلاب خلال مراحل دراستهم لمادة الرياضيات مع عددٍ مختلفٍ من المعادلات الرياضية التي يُطلب منهم حلها كالمعادلات المثلثية، ذات الأهمية البالغة في عددٍ من المجالات كالفيزياء والكيمياء، لكن قد يكون الأمر غايةً في الصعوبة بالنسبة للكثيرين لدرجةٍ قد يؤثر على مستواهم الدراسي؛ لذلك سنحاول من خلال هذه السطور تقديم بعض الأساسيات لمعرفة كيف يتم حل المعادلات المثلثية بالرغم من أنه مجالٌ واسعٌ يحتاج إتقانه وقتًا طويلًا.
ما هي المعادلات المثلثية Trigonometric equations
إحدى أنواع المعادلات الرياضية، تتضمن الدوال المثلثية (Trigonometric Function) وهي Sin وCos وTan، والتي يمكن التحويل بينها لحل المعادلة والوصول إلى قيمة الزاوية المجهولة فيها.
بعض المعادلات المثلثية صحيحةٌ لأي زاويةٍ وتُدعى بالمتطابقة المثلثية (Trigonometric identity)، بينما تنطبق بعض المعادلات على زوايا محددة فقط وتُدعى بالمعادلات الشرطية (Conditional equation).
يمكن حل المعادلات المثلثية ضمن مجالٍ محددٍ يدعى بالحلول الأولية (Primary Solutions)، بينما يكون الحل العام عبارةً عن صيغةٍ تقدّم كافة الحلول الممكنة، ومن المهم معرفة أن الحل لا يعتمد على طرقٍ محددةٍ وخطواتٍ ثابتة؛ حيث تتطلب كل معادلةٍ طريقة حلٍ تختلف عن غيرها، وذلك باستخدام المتطابقات وأساليب الحل الجبرية. [footnote]، Trigonometric Equations، من موقع: www.cliffsnotes.com، اطّلع عليه بتاريخ 11-2-2020[/footnote]
اقرأ أيضًا: الزوايا المثلثية
حل المعادلات المثلثية
كما في المعادلات كثيرة الحدود والمعادلات النسبية، سنصل في نهاية الحل إلى قيمٍ محددةٍ للمتغير فقط، وتُعتبر هي الحل، فعادةً ما تُحل المعادلات المثلثية ضمن مجالٍ محددٍ.
لكن غالبًا ما سيُطلب عند حل المعادلة الوصول إلى كافة الحلول الممكنة، ولأن المتطابقات المثلثية دورية ستتكرر الحلول الناتجة خلال كل مجالٍ؛ بمعنى آخر قد نصل إلى عددٍ غير محدودٍ من الحلول للمعادلات المثلثية، ولذلك يجب تحديد مجال العمل قبل اعتماد أحد الحلول.
لا يختلف حل المعادلات المثلثية عن المعادلات الجبرية، حيث تُقرأ المعادلة من اليسار إلى اليمين بشكلٍ أفقيٍّ، ثم يُبحث في البداية عن النماذج الشائعة والعوامل المشتركة، ثم تُستبدل بعض الصيغ التي تتضمن قيمًا مجهولةً، ليُصبح حل المعادلة بشكلٍ أبسط وبطريقةٍ مباشرة، كما يُمكن الاعتماد على المتطابقات المثلثية في إيجاد الحل.[footnote]، Solving Trigonometric Equations، من موقع: opentextbc.ca، اطّلع عليه بتاريخ 11-2-2020[/footnote]
مبدأ حل المعادلات المثلثية
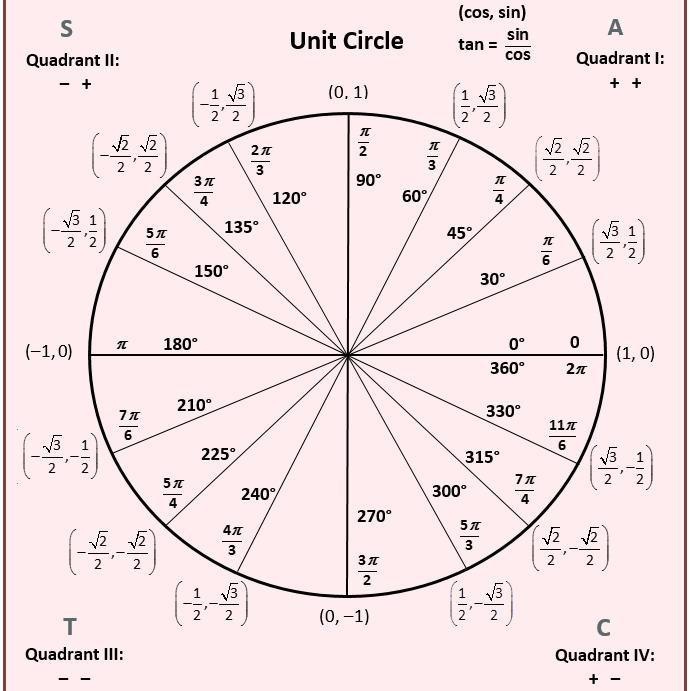
يعتمد حل المعادلات المثلثية على تحويلها إلى إحدى المعادلات المثلثية الأساسية الأربعة وهي Sin(x)=a وCos(x)=a وTan(x)=a وcot(x)=a، والتي يعتمد حلها على دراسة مواقع القوس x في الدائرة المثلثية، واستخدام جدول التحويلات المثلثية أو الآلة الحاسبة.
ولتحويل المعادلة إلى معادلةٍ مثلثيةٍ أساسية يجب الاعتماد على التحويلات الجبرية، وخصائص الدوال المثلثية، والمتطابقات المثلثية، إضافةً للمتطابقات التحويلية.
يجب قبل البدء بحل المعادلة المثلثية إيجاد الأقواس المعروفة بحسب المتطابقات المثلثية، والحصول على قيم تحويل الأقواس من خلال الجداول المثلثية أو الآلة الحاسبة، فمثلًا عند حل المعادلة Cos(x)=0.732 ستُعطي الآلة الحاسبة درجة القوس arc(x)=42.95، بينما من خلال دائرة الوحدة المثلثية سنحصل على كافة الأقواس بنفس قيمة الـ cos.
طرق تحويل المعادلة المثلثية إلى معادلة أساسية
إن تضمنت المعادلة المثلثية دالةً واحدةً، يمكن حلها كمعادلةٍ أساسيةٍ؛ أما إن تضمنت دالتين مثلثيتين أو أكثر، يجب اتباع إحدى الطريقتين بالاعتماد على إمكانية التحويل.
- الطريقة الأولى
يجب تحويل المعادلة إلى معادلةٍ تتطابق مع النموذج F(x).g(x)=0 أو F(x).g(x).h(x)=0، حيث تدل الرموز (f(x و(g(x و(h(x على معادلاتٍ مثلثيةٍ أساسيةٍ؛ فمثلًا لحل المعادلة:
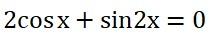
يجب استبدال sin2x باستخدام المتطابقة:

- الطريقة الثانية
تحويل المعادلة المثلثية إلى معادلةٍ أخرى تتضمن دالةً مثلثيةً واحدةً كمتغيرٍ، وأكثر المتغيرات استخدامًا هي;
ثم نقوم بتبسيط المعادلة باستخدام بعض المعادلات في الجبر، وحلها بالاعتماد على الزوايا ضمن المجال 2π ، أما إن ضمت المعادلة الدالة المثلثية tan، سيكون مجال الحل (π). فمثلًا لحل المعادلة:
سنعتمد على بعض العمليات في الجبر بعد اعتبار المتغير هو:
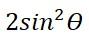
فيكون الحل [footnote]، How to Solve Trigonometric Equations، من موقع: www.wikihow.com، اطّلع عليه بتاريخ 11-2-2020[/footnote]
حل المعادلات المثلثية باستخدام الآلة الحاسبة
لا يمكن حل كافة المعادلات المثلثية دون استخدام الآلة الحاسبة خاصةً تلك التي تتضمن أكثر من زاويةٍ، لذلك يجب في البداية التأكد من ضبط الآلة الحاسبة على الوضع المناسب؛ إما على الدرجات أو الراديان تبعًا للمعادلة، ثم إدخال المعادلة والحصول على النتيجة. في بعض الأحيان يمكن من خلال استخدام بعض العمليات في الجبر تبسيط المعادلة، ثم استخدام الآلة الحاسبة للحصول على الحل الأقرب.
حل المعادلات المثلثية بالشكل التربيعي
قد يعتبر الكثيرون أن حل المعادلات المثلثية التربيعية معقدٌ بعض الشيء بالرغم من إمكانية استخدام العمليات الجبرية في الحل، فإن تضمنت المعادلة دالة مثلثية واحدة مع تربيع إحدى الدالات فيها؛ يمكن حل المعادلة من خلال المعادلات التربيعية النموذجية، ومن خلال استبدال الدالة المثلثية فيها بأحد المتغيرات (مثلًا t) وحلها وكأنها معادلةٌ تربيعيةٌ.
على سبيل المثال لحل المعادلة:
يجب استبدال الدالة cosϴ بالمتغير x لتصبح المعادلة
ثم متابعة الحل كمعادلةٍ تربيعيةٍ. [footnote]، Solving Trigonometric Equations، من موقع: courses.lumenlearning.com، اطّلع عليه بتاريخ 11-2-2020[/footnote]
