ما هي النسبة و التناسب

تم التدقيق بواسطة: فريق أراجيك
غالبًا ما يستخدم الباحثون والرياضيون النسب الرياضيّة لمقارنة المعلومات، فعندما نسمع "بالنسبة إلى" "وجزء من"، فالمقصود هنا من النسبة و التناسب موضوع هذا المقال.
النسبة و التناسب
النسبة
نستخدم النسبة للمقارنة بين شيئين، فعندما نعبر عن النسب بالكلمات نستخدم كلمة "إلى"، أي نقول "نسبة شيءٍ إلى شيءٍ آخر". يمكن كتابة النسب بعدة طرقٍ مختلفةٍ: ككسرٍ أو باستخدام كلمة "إلى" أو بنقطتين.
مثالٌ على ذلك 3 إلى 6، الطريقة الأكثر شيوعًا لكتابة النسبة هي الكسر، 3/6. يمكننا أيضًا كتابتها باستخدام كلمة "إلى" كـ"من 3 إلى 6. " أخيرًا، يمكننا كتابة هذه النسبة باستخدام نقطتين بين الرقمين 3:6. هذه كلها تعطي نفس الفكرة، تعتمد الطريقة التي تختارها على الحالة أو المشكلة.
يوجد هناك طرقٌ أخرى للقيام بالمقارنات، مثل استخدام النسب المتساوية. لإيجاد هذه النسب، يمكن إما ضرب أو قسمة كلّ حدٍّ في النسبة على نفس العدد (ليس الصفر). في مثالنا السابق نسبة 3:6 إذا قسمنا الحدين على الرقم ثلاثة، فسوف نحصل على نفس النسبة، 1:2.

يمكننا أيضًا استخدام الكسور العشرية والنسب المئوية لمقارنة كميتين، في مثال نسبة المربعات إلى الدوائر، يمكننا أن نقول أن عدد المربعات هو "خمسة أعشار" عدد الدوائر، أو 50 ٪.[footnote]، Ratios، من موقع: www.math.com، اطّلع عليه بتاريخ 11-4-2020[/footnote]
التناسب
التناسب عبارةٌ عن مقارنةٍ رياضيةٍ بين رقمين، وفي كثيرٍ من الأحيان يمكن أن تُمثل هذه الأرقام مقارنةً بين الأشياء أو الأشخاص. على سبيل المثال، دخلت غرفةً مليئةً بالأشخاص وتريد أن تعرف عدد الأولاد هناك مقارنة بعدد الفتيات في الغرفة، تُكتب هذه المقارنة في شكل نسبةٍ، تدعى بالتناسب.[footnote]، What is a Proportion in Math? - Definition & Practice Problems ، من موقع: study.com، اطّلع عليه بتاريخ 11-4-2020[/footnote]
التناسب هو ببساطةٍ عبارة عن نسبتين متساويتين، يمكن كتابتها بطريقتين: ككسرين متساويين a/b=c/d، أو باستخدام النقطتين، a_b=d:c، تتم قراءة النسبة التالية كـ "عشرون إلى خمسة وعشرون تساوي أربعة إلى خمسة".
20 /25 = 4 /5
لاختبار ما إذا كانت نسبتان متساويتان في التناسب يمكننا استخدام حاصل الجداء التقاطعي، وللوصول لحاصل الجداء التقاطعي لتناسبٍ ما، نقوم بضرب الحدود البعيدة وتسمى طرفي التّنَاسُب، ونضرب الحدود القريبة وتسمى وسطي التناسب .
هنا، 20 و 5 هما الطرفان، و 25 و 4 هما الوسطَان، نظرًا لأن كلا الجداءين يساويان مائة، فإننا نعرف أن هذه النسب متساوية وأن هذا التناسب حقيقي.
يمكننا أيضًا استخدام الجداء التقاطعي لإيجاد قيمةٍ مفقودةٍ في التناسب، ولنفرض في التناسب السابق أن 4 هو المجهول.
20 /25 = X /5 بالجداء التقاطعي، X.25=5.20 وبالقسمة على 25 نحصل على قيمة 4=X.
أنواع التناسب
التناسب الطَردِيّ
عندما تزيد نسبةٌ تزداد النسبة الأخرى بنفس المعدل والعكس صحيحٌ. مثلًا لتحويل الطول إلى ملم، يكون المضاعف دائمًا 10، يستخدم التَناسُبّ الطَردِيّ لحساب تكلفة البنزين أو أسعار صرف العملات الأجنبية.
حل مسائل التناسب الطردي
الطريقة الأولى
في حالة وجود تناسبٍ طرديٍّ، سيتم إعطاء نسبة واحدة. بعد ذلك، سيتعين علينا استخدام المعادلة أعلاه والعثور على جميع الكميات غير المعروفة، دعنا نفهم هذا بمساعدة مثال:
س: تكلفة 5 كجم من نوعيةٍ معينةٍ من السكر هي 200 دولار، ما تكلفة 1 و2 و 4 و 10 و 14 كجم من السكر من نفس النوع؟
الحل: نرمز x للسكر وy للتكلفة، ونحن نعلم بالفعل أنه مع الزيادة في كمية السكر، فإن تكلفة السكر ستزداد بنفس النسبة، هذه هي القاعدة العامة للتناسب الطردي، الآن، لحل المسألة سنستخدم المعادلة أعلاه:
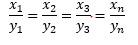
لآن لدينا:
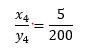
y4= x4*200/5
الطريقة الثانية
نحن نعلم بالفعل أنه في حالة وجود تناسبٍ طرديٍّ x / y=k أيx = k × y. الآن، يمكننا العثور على قيمة k من المعادلة وذلك بتعويض القيم المعروفة مسبقًا، ثم نستخدم المعادلة أعلاه لحساب جميع القيم غير المعروفة.
التَناسُب العكسيّ
عندما تزيد كميةٌ واحدةٌ، تنخفض الكمية الأخرى، والعكس صحيح. على سبيل المثال، زيادة عدد العمال في مهمةٍ ما سيقلل من الوقت، فهي متناسبةٌ عكسيًّا.[footnote]، Direct and inverse proportion ، من موقع: www.bbc.co.uk، اطّلع عليه بتاريخ 11-4-2020[/footnote]
حل مسائل التناسب العكسيّ
الطريقة الأولى
نحن نعلم أنه في النسبة العكسية
x1 y1 =x2 *y2=x3 *y3=x4 *y4
لذلك، عندما يُطلب منك حل هذه المشكلة، يكون لدينا زوجٌ واحدٌ من هذه المعادلة. بعد ذلك يمكننا استخدام المعادلة أعلاه، للعثور على القيم غير المعروفة.
الطريقة الثانية
نعلم أنه في التناسب العكسي، x × y =k. وهذا يعني أن x = k/y، لذلك، للعثور على قيمة k، يمكنك استخدام القيم المعروفة والتعويض من خلال المعادلة أعلاه لحساب جميع القيم غير المعروفة.[footnote]، Direct and Inverse Proportions ، من موقع: www.toppr.com، اطّلع عليه بتاريخ 11-4-2020[/footnote]
 LEAP26
LEAP26 ASUS
ASUS RØDE
RØDE REDMAGIC
REDMAGIC TV
TV Partner With Us
Partner With Us