مساحة شبه المنحرف القائم (مع أمثلة مشروحة)
تم التدقيق بواسطة: فريق أراجيك
تتعدد الأشكال الهندسية في الرياضيات وتتنوع فمنها الثنائي البعد كالمربع والمستطيل والدائرة وشبه المنحرف ومنها الثلاثي الأبعاد كالمكعب والموشور والأسطوانة، في مقالنا التالي سنوضح أحد الأنواع الخاصة لشبه المنحرف وهو شبه المنحرف القائم ، لكن دعونا قبل أن نبدأ بالشرح عنه وكيفية حساب مساحته وحل بعض الأمثلة عنها، دعونا نتعرف أولًا على شبه المنحرف بشكلٍ عامٍّ وأنواعه وخصائصه.
شبه المنحرف
هو شكلٌ هندسيٌّ رباعي الأضلاع، فيه ضلعان متقابلان متوازيان فقط والضلعان الآخران مائلان وغير متوازيين، يشكل هذان الضلعان المتوازيان قاعدتيه والضلعان الآخران يسميان بساقي شبه المنحرف، ويضم أربع زوايا غير متساويةٍ في القياس مجموعها 360 درجةً، بحيث تكون كل زاويتين متتاليتين متكاملتين أي مجموعهما 180 درجةً، أمّا ارتفاعه فهو المسافة الفاصلة بين الضلعين المتوازيين، أي العمود الذي يمتد من القاعدة إلى الجانب الآخر بحيث يشكل معها زاويةً قائمةً.
من الأمثلة الشائعة عن شبه المنحرف هو علبة الفوشار والجسور وحقيبة اليد، وغيرها الكثير من الأشياء التي يمكن أن تصادفنا يوميًّا في حياتنا.
أنواع شبه المنحرف
- شبه المنحرف مختلف الأضلاع (Scalene trapezoid): هو شبه المنحرف الذي تكون أضلاعه الأربعة مختلفةً في الطول، بحيث تكون قاعدتاه متوازيتين لكنهما مختلفتان في الطول وضلعيه الآخرين غير متوازيين وغير متساويين.
- شبه المنحرف متساوي الساقين (Isosceles trapezoid): هو شبه المنحرف الذي تكون ساقاه متساويتين وقاعدتاه متوازيتين ومختلفتين في الطول.
- شبه المنحرف القائم الزاوية (Right Trapezoid): هو شبه المنحرف الذي يحتوي على زاويةٍ قائمةٍ واحدة (90 درجة) بين القاعدة وإحدى ساقيه.
- شبه المنحرف المنفرج الزاوية (Obtuse Trapezoid): هو شبه المنحرف الذي يحتوي على زاويةٍ منفرجة واحدة (أكبر من 90) بين القاعدة وإحدى ساقيه.
- شبه المنحرف الحاد الزاوية (Acute Trapezoid): هو شبه المنحرف الذي يحتوي على زاويةٍ حادةٍ (أصغر من 90) بين القاعدة الكبيرة وإحدى ساقيه..
يوجد بعض الجدل حول هذا السؤال، حيث يرى بعض العلماء أنّ تعريف شبه المنحرف يضم فقط ضلعين متقابلين متوازيين وفي هذه الحالة يكون بالتأكيد متوازي الأضلاع ليس أحد حالات شبه المنحرف، كون تعريف متوازي الأضلاع ينص على أنّه شكل رباعي فيه كل ضلعين متقابلين متوازيين.
بينما رأى البعض الأخر أنّ تعريف شبه المنحرف ينص على أن يحتوي على الأقل ضلعين متقابلين متوازيين، وفي هذه الحالة يمكن اعتبار متوازي الأضلاع هو إحدى حالات شبه المنحرف.
بعض الحقائق الممتعة عن شبه المنحرف
- كان شبه المنحرف يُعرف قديمًا في اللغة اليونانية باسم "τραπέζιον"، الذي تعني حرفيًا "طاولة صغيرة"، وكان يشار إلى أي رباعي أضلاع غير منتظم بـ "oid" والتي تعني "شبه".
- أُدخلت كلمة " trapezium" إلى اللغة الإنجليزية في عام 1570م، وقد كان مارينوس بروكلس أول شخص يستخدم كلمة شبه منحرف في الكتاب الأول لعناصر إقليدس..
شبه المنحرف القائم
كما ذكرنا سابقًا، شبه المنحرف القائم هو إحدى الحالات الخاصة من شبه المنحرف والتي يكون فيها أحد ساقيه عمودي على القاعدتين، أي يشكل معها زاويةً قائمةً.
مساحة شبه المنحرف القائم
لحساب مساحة شبه المنحرف القائم نستخدم القانون الذي يستخدم لحساب مساحة شبه المنحرف العام، الذي ينص على أنّ المساحة تساوي نصف مجموع طولي القاعدتين الصغرى والكبرى مضروبًا بطول الارتفاع، مع وجود اختلافٍ بسيطٍ هو أنّ الارتفاع في هذه الحالة هو الضلع العمودي على القاعدة، وااذي يعبّر عنه وفق ما يلي:
A = (a+b)/2 × h
حيث أنّ:
مثال 1: ليكن لدينا شبه المنحرف القائم في D التالي ABCD، قاعدتيه AB وCD، بحيث AB= 10cm و CD= 14cm وارتفاعه 5cm، احسب مساحته.
الحل: بتطبيق العلاقة السابقة نحصل على:
A = (AB+CD)/2 × AD
A = (10+14)/2 × 5
A = 24/2 × 5 = 60 cm2
إيجاد ارتفاع شبه المنحرف القائم معلوم المساحة
لحساب ارتفاع شبه منحرف معلوم المساحة وطول قاعدتيه، ننطلق من علاقة المساحة ونستنتج الارتفاع (h) لنحصل على العلاقة التالية:
h = 2A/(a+b)
مثال 2: ليكن لدينا شبه المنحرف القائم ABCD مساحته 52cm2، وطول قاعدته الكبرى CD =15cm والصغرى AB =11cm، أوجد ارتفاع شبه المنحرف h..
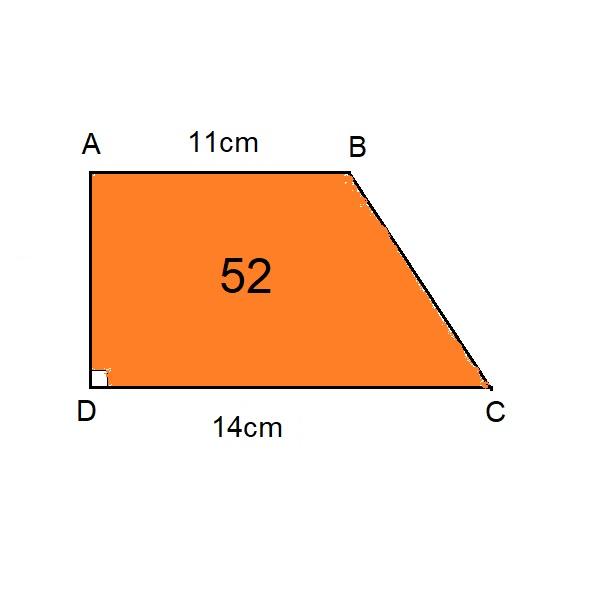
الحل: انطلاقًا من العلاقة السابقة نجد:
h = 2A / (AB+CD)
h = 2(52) / (15 + 11)
h = 104 / 26
h = 4 cm
إيجاد طول قاعدة شبه المنحرف القائم معلوم المساحة
يمكن حساب طول قاعدة شبه المنحرف القائم انطلاقًا من قانون مساحته، إن كان معلوم كل من المساحة والارتفاع وطول القاعدة الأخرى، من خلال العلاقة التالية:
a = (2A/h) - b
مثال 3: ليكن لدينا شبه منحرف قائم ABCD مساحته 40cm2 وطول ارتفاعه h = 4cm وطول قاعدته الصغرى CD = 8cm، أوجد طول قاعدته الكبرى.
الحل: بتطبيق العلاقة السابقة نجد أنّ:
AB = (2A/h) - CD
AB = (2×40/ 4) - 8
AB = 20 - 8 = 12 cm