أشهر المسائل غير المحلولة في الرياضيات.. إن حللتها قد تكسب مبالغ مالية كبيرة!

كلنا نعلم أن الرياضيات صعبةٌ، صعبةٌ جدًا. في الحقيقة هناك صفحةٌ مخصصة حرفيًا من أجل المسائل غير المحلولة في الرياضيات في ويكيبيديا، على الرغم من أن أعظم العقول في العالم تعمل عليها على مدار الساعة لحلها.

ولكن كما يشير لها “أفيري طومسون-Avery Thompson” في الميكانيكا الشعبية من البداية على الأقل، بأن بعض من هذه المشاكل تبدو بشكلٍ مفاجئ بسيطة؛ بسيطةً جدًا في الحقيقة. أيُّ أحدٍ لديه معرفةٌ رياضيةٌ أساسية يستطيع فهمها ومنهم نحن. لكن للأسف تبين أن إثباتها أصعب قليلًا.

الأعداد الأولية هي تلك التي تقبل القسمة فقط على نفسها وعلى الرقم 1، بقدر ما نعرفه هناك عدد لا متناهٍ من الأعداد الأولية، والرياضيون يعملون بجد لإيجاد العدد الأولي الأكبر التالي.

لكن هل يوجد عدد لا متناهٍ من أزواج الأعداد الأولية التي تختلف بمقدار اثنين، مثل 41 و 43؟ كلما كبرت الأعداد الأولية كلما كانت هذه التوائم الأولية أصعب للإيجاد، لكن من الناحية النظرية يجب أن تكون لا نهائية، المشكلة هو أنه لم يستطع أحد إثبات ذلك بعد ولذلك تعد من أهم المسائل غير المحلولة في الرياضيات في التاريخ.

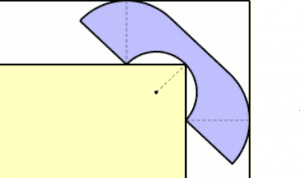
هذا شيءٌ قد عانى منه الكثير منا من قبل، أنت تنتقل إلى شقة جديدة وتحاول إحضار أريكتك القديمة. لكن بالطبع عليك المناورة بها حول الركن قبل أن تشعر بالراحة عليها في غرفة جلوسك.

بدل التخلي عن ذلك و شراء “beanbag”، في هذه المرحلة الرياضيون يريدون أن يعرفوا: ما هي أكبر أريكة من الممكن أن تناسب ركنًا ذا 90° درجة بغض النظر عن الشكل، بدون أن ينحني؟ (على الرغم من أنهم ينظرون إلى الأمر كله من منظور ثنائي الأبعاد)

ويطلق على أكبر مساحة التي يمكن أن تناسب حول الركن –وأنا لا أمازحكم– ثابت الأريكة. لا أحد يعرف على وجه التأكيد كم هو كبير، لكن لدينا بعض الأرائك الكبيرة جدًا التي تعمل، ومنه نحن نعلم أنه على الأقل يجب أن يكون بكبرها. ولدينا أيضًا بعض الأرائك التي لا تعمل ومنه يجب أن يكون الثابت أصغر منها. بجمع كل ذلك؛ نحن نعلم أن ثابت الأريكة يجب أن يكون ما بين 2.2195 و 2.8284. نحن نراهن على أن روس من مسلسل “Friends” تمنى أن يخبره أحدٌ بذلك.

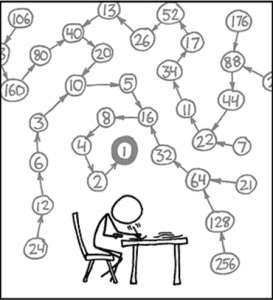
تخمين “Collatz” من أشهر المسائل غير المحلولة في الرياضيات، وهو بسيطٌ جدًا، بإمكانك شرحه لتلاميذ يدرسون في المرحلة الابتدائية، كما أنهم سوف يكونون مفتونين به كفايةً ليحاولوا إيجاد الإجابة بأنفسهم.

إليك كيف يكون: اختر عددًا، أي عدد. إذا كان عددًا زوجيًا اقسمه على 2. وإذا كان فرديًا اضربه في 3 وأضف 1، الآن أعد تلك الخطوات مجددًا بالرقم الجديد الذي حصلت عليه، في النهاية ستحصل على 1 في كل مرة، جربه بنفسك!

على الرغم من البساطة التي يبدو عليها، إلا أن المشكلة أنه بالرغم من أن الرياضيين أظهروا هذا مع الملايين من الأعداد، لم يجدوا أي أعداد لا تلتزم بالقاعدة. من المحتمل أن هناك أعدادًا كبيرةً والتي تؤول إلى النهاية بدل ذلك، أو عدد يعلق في حلقة ولا يصل إلى1. لكن لم يستطع أي شخص إثبات ذلك بشكل مؤكد.

تخمين “Beal” يكون هكذا:

A^X + B^Y = C^Z

و A، B، C، x، y، z كلها أعداد صحيحة موجبة (أعداد صحيحة أكبر من 0)

ثم A، B، C يجب أن يكون لها كلها عامل مشترك رئيسي، العامل المشترك الرئيسي هو أنه يجب أن يكون على كل من هذه الأعداد قابلية القسمة على نفس العدد الأولي، إذًا الأعداد 15، 10 و5 لها عامل مشترك رئيسي (لهم قابلية القسمة على العدد الأولي 5)

إلى حد الآن الأمر سهل، ويبدو كشيءٍ كنت تستطيع حله بالجبر الذي درسته في الثانوية. لكن ها هي المشكلة، الرياضيون لم يستطيعوا أبدًا حل تخمين “Beal” مع كون كل من x ، y ، z أكبر من 2.

على سبيل المثال؛ لنستعمل أعدادنا ذات العامل المشترك الرئيسي 5 من السابق:

5¹+10¹=15¹

لكن 5²+10²=15²

يوجد حاليًا جائزةٌ تقدر بمليون دولار، لأيِّ شخصٍ يتمكن من تقديم إثباتٍ مراجعٍ مسبقًا لهذا التخمين، إذًا ابدأ بالحساب.

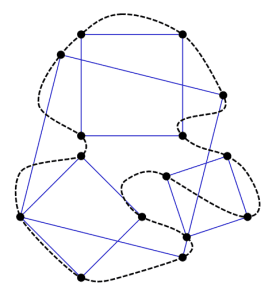
هذا يتطلب القليل من الرسم، على قطعة من الورق، ارسم حلقة، لا يجب أن تكون ذات شكل متقن، فقط حلقة مغلقة لا تعبر نفسها.

وفقًا لفرضية مربع المدرج، داخل تلك الحلقة بإمكانك رسم مربع كل رؤوسه الأربعة تمس الحلقة. مثل ما يبينه الرسم البياني فوق.

تبدو سهلةً، لكن لنتكلم رياضيًا، يوجد هناك الكثير من أشكال الحلقات وهو أمر مستحيل أن نقول أن هناك مربع يستطيع لمس كل منهم. سبق هذا وأن تم حله بالنسبة لعدد من الأشكال مثل المثلثات والمستطيلات. لكن المربعات مخادعة، حتى الآن الإثباتات الرسمية استعصت على الرياضيين.

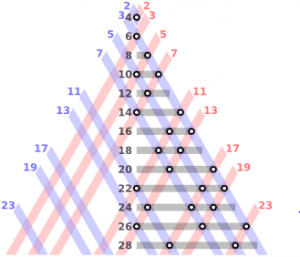
وهو مشابهٌ لـتخمين التوائم الأولية، تخمين “غولدباخ” هو سؤال آخر عن الأعداد الأولية يبدو سهلًا وهو مشهور بمدى سهولته ومخادعته.

ها هو السؤال: هل كل عدد أكبر من 2 هو مجموع عددين أوليين؟

يبدو أمرًا بديهيًا أن تكون الإجابة بنعم، بعد كل شيء 1+ 2 = 3 ، 3+1=4 وهكذا دواليك.

لكن مجددًا، لم يستطع أحد إثبات أن هذه الحالة، بالرغم من سنوات من التجريب.

الحقيقة هو أنه إذا أتممنا الحساب بأعدادٍ أكبر فأكبر فإننا قد نصل في النهاية إلى عددٍ ليس مجموع عددين أوليين أو عدد يتحدى كل القواعد والمنطق لدينا حتى الآن. ويمكنك أن تكون متأكدًا أن الرياضيين لن يتوقفوا عن البحث حتى يجدوا إثباتًا.

أعلن معهد كلاي في 24 مايو 2000 عن جائزة مالية قدرها مليون دولار أمريكي لمن يقدم حلاً صحيحاً لحدسية هودج، حيث تعتبر حدسية هودج من أكثر المسائل غير المحلولة في الرياضيات صعوبةً في مسائل الألفية لمعهد كلاي؛ لأنها تحتاج إلى معرفة متقدمة في عدة حقول في الرياضيات وهي التوبولوجيا والهندسة الإقليدية والجبر والتحليل. وقد سميت هذه الحدسية بهذا الاسم نسبةً إلى صاحبها عالم الرياضيات الأسكتلندي وليام فالانس دوغلاس هودج والذي أعلن عنها عام 1950.

لعلنا نتذكر تلك المعادلة y=X² والتي ينتج عند التعويض بمجموعة من النقاط. في هذه المعادلة منحى مميز يسمى القطع المكافئ، والمعادلة X²+y²=1 ينتج عنها رسم دائرة. الشكل الجبري يتعامل مع الأبعاد الأعلى المماثلة لذلك النوع من المنحنيات حينما نتعامل مع نظام متعدد المعادلات أو معادلات ذات أكثر من متغير أو معادلات على مستوى الأعداد المركبة (التخيلية).

في القرن العشرين اكتشف الرياضيون طرق للتحقق من الصيغ الرياضية لأشكال معقدة، متسائلين إلى أي مدى يمكننا الاقتراب من الصيغة الرياضية الحقيقية لأي شكلٍ معقد، وذلك بتجميع عدة أشكال هندسية بسيطة بالتزامن مع زيادة أبعادها.

لاحقاً تم اعتماد هذا المبدأ واستخدامه في مسائل كثيرة وبطرق مختلفة مكنت الرياضيين من القيام بعمليات فهرسة وتصنيف جميع العناصر والأشكال التي ظهرت خلال أبحاثهم الرياضية. الأساس الهندسي لهذا المبدأ مازال مبهماً بل أحياناً كان من الضروري إضافة قطع دقيقة من أشكال معينة ليس لها أساس هندسي معروف. حدسية هودج، التي تعد من أبرز المسائل غير المحلولة في الرياضيات تؤكد فعالية هذا المبدأ من أجل الأنواع البسيطة من الفضاءات الجبرية المتعددة وتسمي هذه القطع الدقيقة بحلقات هودج وهي في الحقيقة صيغة رياضية من الجبر الخطي مصاغة من قطع هندسية تسمى الحلقات الجبرية.

ترتبط نظرية يانج-ميلز بنظرية الحقل الكمومي التي مكنت الفيزيائيين من تحقيق العديد من النجاحات باستخدام هذه النظرية، فالعديد من الحسابات المبنية عليها أعطت نتائج متوافقة مع التجارب حتى الآن، ورغم ذلك فالأساس الرياضي لهذه النظرية لازال غير مفهومٍ بشكل كامل.

فعندما قام علماء الفيزياء بمراقبة التفاعلات النووية الشديدة لم يجدوا جسيمات عديمة الكتلة كما كانت النظريات الكلاسيكية تتنبأ، فاستحدثوا مصطلحات جديدة مثل “فجوة الكتلة” الموجودة فقط في نظيرتها الكمومية. فكانت الحاجة لمقاربة مبنية بشكل دقيق رياضياً لنظرية يانج-ميلز الكمومية؛ وحتى يومنا هذا لا نملك الرياضيات اللازمة لفعل ذلك. رغم كفاءة النظرية الكمومية بشكلها الحالي لوصف الواقع،

فالمطلوب من حل هذه المسألة الرياضية، هو إيجاد تفسير وجود ” فجوة الكتلة” في نظرية يانج-ميلز الكمومية، وهذا يتطلب صياغة للنظرية في أربعة أبعاد لتفسير خاصية وجود فجوة الكتلة.

نظرية يانج- ميلز هي نظرية فيزيائية، ولكنها ذات أهمية كبيرة أيضاً بالنسبة لعلماء الرياضيات، وذلك لأن الفيزيائيون قاموا بوضع أدوات لإجراء حساباتهم ضمن نظرية الحقل الكمومي، وقدمت هذه الأدوات توقعات دقيقة في مجال الهندسة والتوبولوجيا، وبخاصة عندما يكون عدد الأبعاد منخفضة. ولكن هذه الأدوات ليست واضحة بشكل قوي رياضياً إلا في حالات بسيطة، وهذا يدل على أن هناك مجموعة كبيرة من الطرق الفعالة في الرياضيات بانتظار من يكتشفها، وبحل هذه المسألة من المسائل غير المحلولة في الرياضيات نتوقع اكتشاف بعضها.

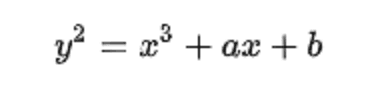
دراسة المنحنيات الإهليجية دراسة ممتدة عبر تاريخ طويل وحافل منذ القدم وحتى يومنا هذا، حيث أنها متواجدة في العديد من فروع الرياضيات الحديثة، وخاصةً في نظرية الأعداد. المنحنى الإهليجي هو منحنى جبري ناعم، يمكننا أن نضعه في الصيغة الرياضية التالية:

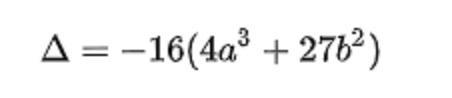
ولكي يكون المنحنى ناعماً، لابد وأن يكون المميز الموضح في الصيغة التالية لا يساوي صفراً:

وعند وضع a= -1 و b = 0 سيكون الناتج كما هو موضح في الصورة التالية:

نلاحظ بأن p4=p1+p2، إن مجموعة النقاط الكسرية مع عملية الجمع تشكلان ما يسمى بالزمرة. كان لويس موريديل وأندريه وايل أول من حددا بنية هذه الزمرة من النقاط الكسرية وأثمرت جهودهما بنظرية سميت باسمها، نظرية موردل- وايل في عام 1922.

ليومنا هذا لا توجد خوارزمية عامة ومعروفة لتحديد رتبة المنحنى الإهليجي، وإن كان هناك وسائل تطبق على بعض الحالات فقط، كما أن لكل منحنى إهليجي E تابع عقدي بمتغير s يعرف بالدالة اللامية E(L,s)‎. اكتشف العالمان بريش وداير من خلال التجارب ما يسمى بالدالة اللامية للمنحنى الإهليجي، والتي تنص على أن درجة انعدام التابع E(L,s)‎ عند النقطة s=1 مرتبط ببعد الشبكية والموجودة في زمرة النقاط الكسرية. وقد تم إجراء هذا بالتجربة ولكن ليس بالبرهان الرياضي

لهذه الحدسية، التي تعتبر من أهم المسائل غير المحلولة في الرياضيات ميزة رائعة حيث تربط بين عالم الجبر حيث معادلات كثيرات الحدود وعالم التوابع العقدية حيث تنتمي الدالة اللامية ولا عجب أنها ساهمت في تطوير نظرية الأعداد.

قبل الحديث عن معادلات نافييه-ستوكس لابد وأن نلقي الضوء على الموائع والتي هي مادة قادرة على أخذ شكل الإناء الذي توضع فيه، فالغازات والسوائل تعتبر موائع لاتخاذها شكل الإناء التي توضع فيه بعكس الأجسام الصلبة التي لا تتبع نفس السلوك. أما اضطراب الموائع فهو حركة معقدة فوضوية للمائع، وهو موجود في كل مكانٍ حولنا، فقط لوح بيدك الآن أمام وجهك وتكون قد صنعت اضطراب، صحيح أنه اضطراب بسيط، لكن هناك اضطرابات مزعجة للبعض مثل اضطراب حركة الطائرات في الرحلات الجوية والأعاصير وشلالات المياه.

ولكي يعتبر الاضطراب مشكلة قابلة للحل في الفيزياء نحتاج إلى وضع معادلة تصف حركة المائع ثم حلها للتنبؤ الدقيق بكيفية تحرك المائع تحت مجموعة معينة من الظروف. الصيغة الأكثر قبولاً لوصف اضطراب الموائع هي معادلات نافييه-ستوكس، وقد تم الحصول عليها من تطبيق قانون نيوتن الثاني على الموائع، ولهذه المعادلات عدة صيغ مختلفة يمكننا كتابة هذه المعادلات بها منها ما هو موضح أدناه:

F: محصلة القوى المؤثرة على المائع

u: تأثير الكتلة

ρ: الكثافة

p: الضغط المؤثر على المائع

من الصعب حل معادلات نافييه-ستوكس لأنها معادلة غير خطية، بمعنى آخر إن وجود تغيير بسيط في الحالة الأولية للنظام يؤدي إلى تغيير شديد في النتائج يصعب التنبؤ به بدقة. بعكس معادلة الموجات الصوتية على سبيل المثال فهي معادلة خطية لذا يمكنك بناء صوت معقد من خلال الجمع بين العديد من الأصوات البسيطة ويمكننا التنبؤ بالنتائج. ولذا ليس من المستغرب أن تكون معادلات نافييه-ستوكس من المسائل غير المحلولة في الرياضيات.

في عام 2014 تناقلت وكالات الأنباء عن خبر ادعاء عالم الرياضيات الكازاخستاني ”مختار باي أوتيلبايف” الأستاذ في معهد الرياضيات والتصميم الرياضي التابع لوزارة التعليم في جمهورية كازاخستان، أنه وجد حلاً لمعادلات نافييه – ستوكس، وذلك في مقال نشره بمجلة الرياضيات، وأن العلماء الكازاخستانيين بحثوا هذا الحل واعتبروه صحيحاً لكن على ما يبدو لم يحظى الحل بالقبول المطلوب من قبل علماء ومؤسسات الرياضيات الكبرى في العالم.