المتتالية الهندسية.. ماهي؟

تم التدقيق بواسطة: فريق أراجيك
ما هي المتتالية الهندسية؟، إذا أخذنا ورقة وقمنا بطيها عدد من المرات، هل يمكننا حساب ارتفاع الورقة بعد طيها لخمس أو ست مرات مثلاً؟ بالتأكيد يمكن ذلك من خلال استخدام قواعد المتتالية الهندسية ، لكن ما هي هذه المتتاليات؟ هذا ما سنقوم بدراسته بالتفصيل في مقالنا التالي، لكن لنقم بدايةً بالتعرف على المتتاليات الرياضية بشكل عام.
المتتالية الهندسية: تعريف المتتاليات
تُعرف المتتاليات في الرياضيات على انها عبارة عن مجموعة من الأرقام أو الأحداث المرتبة وفق تسلسل معين اعتماداً على بعض القواعد الأساسية، فإذا كان لدينا المحارف a1 وa2 وa3 تدل على حدود المتتالية فإن الأرقام 1 و2 و3 تدل على دليل الحد أي موضع الحد ضمن المتتالية، بناءً على عدد حدود المتتالية يمكن تحديد إن كانت هذه المتتالية محدودة (لها عدد حدود معين) أو غير محدودة (تملك عدد غير نهائي من الحدود).
مجالات المتتالية
هناك مجالات وفوائد عديدة للمتتاليات سواء في الرياضيات أو في الحياة العامة ومن أشهر مجالات استخدامها
التحليل الرياضي
خاصة في مجال دراسة المعادلات التفاضلية حيث نحصل على حلول هذه المعادلات في الكثير من الأحيان نهايات متتاليات تقربنا شيئاً فشيئاً من الحل الدقيق
كذلك في الحساب أو التحليل العددي: كالتقريبات وتقديرات الأخطاء التي تتم عموماً عبر المتتاليات.
تعريف مفاهيم رياضية أخرى كالانتقال مثلاً من تعريف مفهوم المكاملة للدالة معرفة على مجال حقيقي وتأخذ قيمها في فضاء مجرد.
مثل فضاء باناخ الذي يمر عبر المتتاليات
ومن التطبيقات التي نجدها في المتتاليات أنها تمكن من تعريف العديد من الدوال المألوفة مثل:
الدالة الأسية.
الدالة المثلثية جيب
الدالة المثلثية تجب
الدالة اللوغاريتمية بوصفها الدالة العكسية للدالة الأسية
الدالة المثلثية ظل بوصفها نسبة للدالتين المثلثيتين جيب وتجب
كذلك تستخدم المتتاليات في مجالات البرمجة الحاسوبية
كما تظهر أهمية المتتالية الهندسية من الناحية التطبيقية في مادة الرياضيات المالية عند دراسة الفائدة والجملة والقيمة الحالية لمبلغ ما أو للدفعات المؤكدة المتساوية بفائدة مركبة خصوصاً في الحالات التي يكون فيها كل من معدل الفائدة أو المدة غير موجودين أصلاً أو في الحالات التي تكون فيها كل من معدل الفائدة أو المدة غير موجودين في جدول فائدة مركبة وكذلك استهلاك الأصول مما يجعل للمتتالية الحسابية أهمية كبيرة
ما هي المتتالية الهندسية؟
نقول عن متتالية أنها متتالية هندسية عندما نحصل على حدودها من خلال
ضرب أو قسمة الحد الأول بقيمة ثابتة لنحصل على الحد الثاني وهكذا تعاد الكّرة في
كل مرة حتى نصل إلى نهاية المتتالية، تسمى القيمة الثابتة التي يتم الضرب بها
بالنسبة أو العامل المشترك ويرمز لها بالرمز r.
يجب أن يكون الحد الأول في المتتالية غير صفري حتماً لأن عكس ذلك يعني أن جميع حدود المتتالية متساوية وصفرية وهذا ما يخالف الشرط الأساسي لكونها متتالية هندسية وهو أن كل حد يساوي الحد الذي يسبقه مضروباً أو مقسوماً على النسبة المشتركة r.
على سبيل المثال تشكل سلسلة الأرقام 1، 2، 4، 8، 16، 32 متتاليةهندسية حيث نتج كل رقم عن الرقم السابق له بضربه بـ 2 أي أن النسبة المشتركة هي r = 2، لكن كيف علمنا قيمة r؟
الحد الأول في المتتالية هو a1=1 والحد الثاني هو a2=2 إذا قسمنا a2 على a1 نحصل على:
وإذا أوجدنا نسبة a3 على a2 نلاحظ أنها:
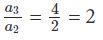
وكذلك:
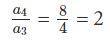
بالتالي نستنتج أن:
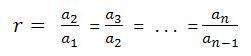
حيث:
- an-1: يمثل الحد قبل الحد الأخير من المتتالية.
- an: يمثل الحد الأخير من المتتالية.
أي أن نسبة أي حدين على التوالي من هذا
المتتالية هي قيمة ثابتة.
الصيغة العامة لـ المتتالية الهندسية
يمكن إيجاد الصيغة العامة للمتتالية من خلال ملاحظة أن كل حد من حدود المتتالية ينتج عن الحد الأول وفق ما يلي:
A1= a1
A2 =a1 × r
A3= a2 × r =( a1× r) × r= a1× r2
A4 = a3× r = (a1× r2) × r =a1× r3
بالتالي نستنتج أن:[footnote]، Geometric Progression، من موقع: www.toppr.com، اطّلع عليه بتاريخ 1-3-2020[/footnote]
an= a1× rn-1
مجموع حدود المتتالية الهندسية
يمكن إيجاد مجموع حدود المتتالية بسهولة من خلال استخدام الصيغ التالية:
- إذا كان عدد حدود المتتالية معلوم (n حد) نستخدم الصيغة التالية:
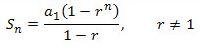
- إذا كان المتتالية ذات عدد لا نهائي من الحدود نستخدم الصيغة التالية:
حيث ان:
- Sn: مجموع المتتالية عند عدد حدود n.
- ∞S: مجموع المتتالية الغير محدودة.
- n: عدد الحدود.
اقرأ أيضًا: الفرق بين المتتالية الهندسية والمتتالية الحسابية.
خصائص المتتالية الهندسية
- إذا كان لدينا متتالية نوعها هندسية وقمنا بضرب أو قسمة كل عنصر من عناصرها بعدد معين غير صفري فإن المتتالية الناتجة هي متتالية نوعها هندسية أيضاً.
- إذا كان لدينا متتالية نوعها هندسية أولى .....,a1,a2,a3,a4 ومتتالية نوعها هندسية ثانية ….,b1,b2,b3,b4 فإن المتتالية الناتجة من ضرب كل عنصر من عناصر المتتالية الأولى بالعنصر المقابل له من المتتالية الثانية هي متتاليية هندسية أيضاً.
- إذا كان لدينا ثلاث أعداد a,b,c من متتالية نوعها هندسية فإن b2=a×c
أنواع أخرى من المتتاليات
يوجد الكثير من الأنواع للمتتاليات
الرياضية أهمها:
- المتتالية الحسابية: نقول عن متتالية أنها حسابية عندما يتم الحصول عليها من خلال إضافة أو طرح رقم معين من الرقم الذي يسبقه.
- المتتالية التوافقية: نقول عن متتالية أنها توافقية إذا كان مقلوب جميع عناصرها (حدودها) هو عبارة عن متتالية حسابية.
- متتالية فيبوناتشي أو أعداد فيبوناتشي: يتم الحصول على كل حد من حدود متتالية فيبوناتشي من خلال إضافة الحدين السابقين له، يتم في البداية استخدام الرقمين 0 و1 بحيث يكون F0 = 0 و F1 = 1 بالتالي يتم التعبير عن متتالية فيبوناتشي بالشكل:
Fn = Fn-1 + Fn-2
