حجم هرم قاعدته مربع (مع أمثلة مشروحة)
تم التدقيق بواسطة: فريق أراجيك
الهرم شكلٌ هندسيٌّ متعدد الأوجه، يتألف من قاعدةٍ وأوجهٍ جانبيةٍ تصل كل منها بين قمة الهرم وحرفٍ من أحرف القاعدة، يبلغ عدد هذه الأحرف الجانبية ثلاثًا أو أكثر، يتخذ كل وجهٍ من الأوجه شكل مثلث، وتتلاقى قمة المثلثات مع بعضها في نقطةٍ واحدةٍ تدعى بقمة الهرم (Apex). قد تتخذ قاعدة الهرم شكل أي مضلعٍ هندسيٍّ، وعدد الأوجه في الهرم مساوي لعدد أضلاع قاعدته، يطلق على هذه المثلثات مصطلح أوجه جانبية للهرم، لتمييزها عن قاعدته، في حال كانت القاعدة على شكل مثلثٍ. موضوع مقالنا هذا عن كيفية حساب حجم هرم قاعدته مربع حصرًا، ولكن قبل أن نبدأ؛ يجب أن تعرف أن للهرم نوعان:
- الهرم القائم (Right Pyramid): يكون الهرم قائمًا عندما يلتقي العمود النازل من قمة الهرم، مع قاعدته في منتصفها.
- الهرم المائل (Oblique Pyramid): يطلق على الهرم مصطلح الهرم المائل عندما يكون العمود النازل من القمة إلى قاعدة الهرم، يقع في أي نقطةٍ من القاعدة إلّا منتصفها.[footnote]Volume and Surface Area of a Pyramid، من موقع: www.math-only-math.com، اطّلع عليه بتاريخ August/12/2020 | 04:43 PM[/footnote] [footnote]Problems on Pyramid، من موقع: www.math-only-math.com، اطّلع عليه بتاريخ August/12/2020 | 04:43 PM[/footnote].
حجم هرم قاعدته مربع
القانون المستخدم في حساب حجم الهرم هو ذاته أيًا كان نوع الهرم، وشكل قاعدته، وعدد أوجهه الجانبية، إذًا يكون قانون حجم الهرم:
حجم الهرم= ⅓ مساحة القاعدة * ارتفاع الهرم
حيث ارتفاع الهرم هو العود النازل من قمة الهرم إلى قاعدته.
في حالة الهرم ذو القاعدة على شكل مربع، وبالتعويض في قوانين المساحة، يصبح قانون حجم هرم قاعدته مربع هو:
حجم هرم قاعدته مربع = ⅓ (طول ضلع القاعدة)2 * الارتفاع
قوانين وملاحظات إضافية
- في حال كان الهرم قائمًا، وقاعدته على شكل مربعٍ، تكون المثلثات الأربعة التي تشكل الأوجه الجانبية له متطابقةً ومتساوية الساقين.[footnote]Volume of a Pyramid، من موقع: www.mathsteacher.com.au، اطّلع عليه بتاريخ August/12/2020 | 04:42 PM[/footnote][footnote]Pyramid، من موقع: www.mathopenref.com، اطّلع عليه بتاريخ August/12/2020 | 04:41 PM[/footnote].
- مساحة الهرم = مساحة وجوهه الجانبية + مساحة القاعدة.
- مساحة الوجوه الجانبية = ½ * محيط القاعدة * الارتفاع الجانبي.
- الارتفاع الجانبي هو العمود النازل من قمة الهرم على ضلع قاعدته.[footnote]Volume of a Pyramid، من موقع: byjus.com، اطّلع عليه بتاريخ August/12/2020 | 04:43 PM[/footnote][footnote]Surface Area of a Pyramid، من موقع: www.varsitytutors.com، اطّلع عليه بتاريخ August/12/2020 | 04:42 PM[/footnote]
- مساحة هرم قاعدته مربع = (طول ضلع قاعدته)2 + 2 * طول ضلع القاعدة * الارتفاع الجانبي للهرم.[footnote]Surface Area of A Pyramid، من موقع: www.onlinemathlearning.com، اطّلع عليه بتاريخ August/12/2020 | 04:42 PM[/footnote].
أمثلة محلولة لحساب حجم هرم قاعدته مربع
حجم الهرم = ⅓ مساحة القاعدة * ارتفاع الهرم
مساحة قاعدة الهرم = (طول الضلع)2
مساحة قاعدة الهرم = 4 * 4= 16 سم2.
ويكون حجم هرم قاعدته مربع = ⅓ * 16 * 9= 48 سم3.
حجم الهرم = ⅓ مساحة القاعدة * ارتفاع الهرم
حجم الهرم = ⅓ (10)2 * 18
حجم الهرم = ⅓ * 100 * 18= 600 سم3.
مساحة الأوجه الجانبية للهرم= ½ * محيط القاعدة * الارتفاع الجانبي.
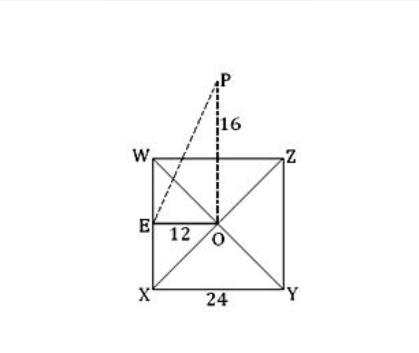
يوضح الشكل المربع WXYZ والذي يشكل قاعدة الهرم، والنقطة O هي نقطة تلاقي قطريه WY و XZ، أما PO فهو العمود النازل من قمة الهرم إلى منتصف قاعدته، أي أن OP هو ارتفاع الهرم.
يُرسم عمود OE من النقطة O باتجاه الضلع WX، ليكون بذلك OE=EX= 1/2*WX= 12.
نستنتج مما سبق بأن PE هو الإرتفاع الجانبي للهرم، ولحساب طوله نقوم بتطبيق نظرية فيثاغورث في المثلث POE والقائم في O:
PO2 + OE2 = PE2
PE2= 162 + 122
PE2= 256 + 144
PE2= 400
سم PE= √400= 20
بالتعويض في المعادلة نجد ما يلي:
مساحة الأوجه الجانبية للهرم = ½ * (24 * 4) * 20
مساحة الأوجه الجانبية للهرم = 960 سم2.
المساحة الكلية لسطح الهرم = مساحة القاعدة + مساحة الأوجه الجانبية للهرم
المساحة الكلية لسطح الهرم = 242 + 960
المساحة الكلية لسطح الهرم = 1536 سم2.
حجم الهرم = ⅓ مساحة القاعدة * ارتفاع الهرم
حجم الهرم = ⅓ * 242 * 16
حجم الهرم = 3072 سم3.
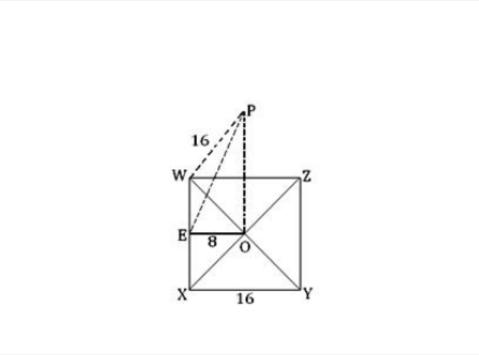
المربع WXYZ هو قاعدة الهرم، وO هي نقطة تلاقي القطرين WY وXZ، وOP هو العمود النازل من قمة الهرم على قاعدته، فيكون هو ارتفاع الهرم.
كون الأوجه الجانبية للهرم مثلثات متساوية الأضلاع يعني أن: PW = WX = XY = YZ = ZW=16. بتطبيق نظرية فيثاغورث في المثلث WXY القائم في X نجد ما يلي:
WY2 = WX2 + XY2
WY2 = 162 + 162
WY2 = 256 + 256
WY2 = 512
WY = √512 = 16√2
WO=½ * 16√2= 8√2.
بتطبيق نظرية فيثاغورث في المثلث POW القائم في O ستظهر المعادلة التالية:
OP2 + OW2= PW2
OP2= PW2 - OW2
OP2= 162 - (8√2)2= (8√2)2
OP = 8√2.
برسم المستقيم OE العمود على WX، نلاحظ أن طوله يساوي نصف طول ضلع القاعدة، أي يساوي 8.
مما سبق نستنتج أن PE هو الارتفاع الجانبي للهرم، ولحسابه، نستخدم نظرية فيثاغورث في المثلث POE القائم في O:
PE2= PO2 + OE2.
PE2= (8√2)2 + 82.
PE2= 128+ 64.
PE2= 192.
PE= 8√3.
المساحة الكلية للهرم = مساحة الأوجه الجانبية + مساحة القاعدة.
المساحة الكلية للهرم = ½ * محيط القاعدة * الارتفاع الجانبي + (طول الضلع)2، وبالتعويض نجد:
المساحة الكلية للهرم = 256(1 + 3√) سم2.
حجم الهرم = ⅓ * مساحة القاعدة * ارتفاع الهرم
حجم الهرم = ⅓ * 162 * 2√8
حجم الهرم = ⅓ * 2√2048 سم3.
