مساحة المعين (مع أمثلة مشروحة)
تم التدقيق بواسطة: فريق أراجيك
المعين هو عبارةٌ عن شكلٍ هندسيٍّ مضلع ثنائي الأبعاد، يُستخدم في الكثير من المجالات والتطبيقات في مجال الرياضيات وفي حياتنا العلمية والعملية، وتُعرف مساحة المعيّن على أنها المساحة المحدودة بأضلاع المعين، أي داخل محيط المعين، ويوجد عدة قوانين وطرقٍ رياضيةٍ لحساب مساحة المعين سوف نشرحها بالتفصيل في هذا المقال مع ذكر بعض الأمثلة.
تعريف المعين وأهم صفاته
المعين هو من الأشكال الهندسية الرباعية؛ أي أنه يتكون من أربعة أضلاع، وهو يشبه متوازي الأضلاع، لكن يختلف عنه في أن أطوال أضلاعه تكون متساويةً، له أربع زاويا، كل زاويتين متقابلتين فيه تكون متساويتين، وكل ضلعين متقابلين فيه متوازيان.
يختلف المعين عن المربع أيضًا بأن زواياه غير قائمةٍ، بينما زوايا المربع جميعها متساوية وقائمة، لذا يصبح المعين مربعًا عندما تكون زواياه قائمة، وبعبارةٍ أخرى يمكننا القول بأن: "كل مربعٍ هو معين ولكن كل معينٍ ليس مربعًا".
يتميز المعين أيضًا بأن له قطرين الأطول d1 والأصغر d2 -والقطر هو أي قطعةٍ مستقيمةٍ تصل بين زاويتين متقابلتين-، قطراه متعامدان ويتقاطعان في منتصفه، كما أنهما ينصفان كل زواياه الداخلية.
أمثلة من الحياة الواقعية
يمكن رؤية شكل المعين في مجموعةٍ متنوعةٍ من الأشياء في عالمنا المحيط، مثل الطائرة الورقية، ونوافذ السيارة، إشارات المرور، بعض المجوهرات تكون على شكل معينٍ، أيضًا هيكل المباني، المرايا...[footnote]Rhombus - Definition with Examples، من موقع: www.splashlearn.com، اطّلع عليه بتاريخ August/29/2020 | 02:45 PM[/footnote].
طرق حساب مساحة المعين
1. مساحة المعين بدلالة طول قطريه
يمكن حساب مساحة المعيّن إذا كانت أطوال أٌقطاره معلومة وفق العلاقة الرياضية التالية:
مساحة المعين = القطر الأول × القطر الثاني ÷2
S = ½ × d1 × d2
2. مساحة المعين بدلالة القاعدة والارتفاع
مساحة المعين = القاعدة × الارتفاع
S = b × h
قاعدة المعين هي أحد أضلاعه حيث يمكن استخدام طول أي ضلعٍ، لأنه كما ذكرنا سابقًا أضلاع المعين متساوية في الطول، والارتفاع هو المسافة العمودية من القاعدة المختارة إلى الجانب المقابل.
3. مساحة المعين بدلالة القاعدة والمحيط
S = 2b × r
4 . مساحة المعين بدلالة جيب أحد الزوايا والمحيط
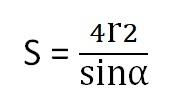
5. بدلالة القطر وظل نصف الزاوية
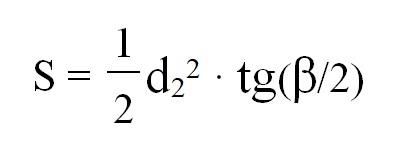
6. بدلالة جيب الزاوية وطول أحد الأضلاع
مساحة المعين = جيب الزاوية a × مربع طول الضلع
(S = b2 × Sin(a
حيث إن:
- S: مساحة المعيّن.
- b: طول أحد الأضلاع.
- r : محيط المعين.
- h: الارتفاع.
- a : الزاوية المحصورة بين ضلعين متجاورين.
نختار الطريقة المناسبة لحساب مساحة المعين حسب المعطيات الموجودة في المسألة، وسنشرح ذلك بأمثلةٍ في الفقرة التالية.[footnote]Rhombus. Formulas, characterizations and properties of rhombus، من موقع: www.onlinemschool.com، اطّلع عليه بتاريخ August/29/2020 | 02:45 PM[/footnote].
أمثلة على حساب مساحة المعين
ليكن المعين ABCD، الذي له قطران، أي AC و BD
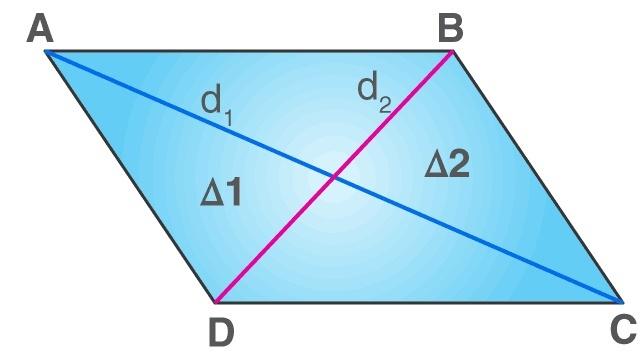
مثال 1
احسب مساحة المعين ذي الأقطار التي تساوي 6 سم و 8 سم.
الحل:
بما أن القطر الأول cm d1 = 8، والقطر الثاني cm d2 = 6
نطبق العلاقة S= ½ × d1 × d2
S = (d1 × d2) / 2
= (6 × 8) / 2
= 48/2
= 24 cm2
وبالتالي فإن مساحة المعيّن تساوي 24 cm2.
مثال 2
احسب مساحة المعيّن إذا كانت قاعدته 10 سم وارتفاعه 7 سم.
الحل :
لدينا المعطيات التالية:
القاعدة سم b = 10
الارتفاع سم h = 7
لذا نطبق العلاقة التالية: S = b × h
70 سم = 10 × 7= S
مثال 3
احسب مساحة المعين إذا كان طول ضلعه 2 سم وإحدى زاوياه 30 درجةً.
الحل:
المعطيات المعلومة هي:
القاعدة أو (طول الضلع) = 2 سم ، الزاوية a = 30
لذا نطبق العلاقة: (S= b2 × Sin(a
b2 = 2 × 2 = 4
(S=4 × sin (30
S=4×12
S=2cm2. [footnote]Area Of Rhombus، من موقع: www.byjus.com، اطّلع عليه بتاريخ August/29/2020 | 02:45 PM[/footnote].
مثال 4
أوجد مساحة المعين التي يساوي كل ضلعٍ منها 17 سم وأحد قطريها يساوي 16 سم.
الحل:
ABCD معين، حيث: سم AB = BC = CD = DA = 17
أحد قطريه AC= 16 سم مع كون O نقطة التقاطع القطرية، لذا فإن نصف القطر 8 سم =AO
علينا أولًا حساب طول القطر الثاني BD للمعين لكي نستطيع تطبيق العلاقة: S= (d1 × d2) / 2.
كما ذكرنا سابقًا أن قطري المعين متعامدان، وبالتالي فإن تقاطعهما يقسم المعيّن إلى 4 مثلثاتٍ قائمة الزاوية.
لدينا المثلث القائم ∆ AOD، وحسب نظرية فيثاغورث المعروفة والتي تنص على أن: مربع طول الوتر في المثلث القائم يساوي مجموع مربعي الضلعين المجاورين للزاوية القائمة.
وبالتالي فإن:
AD2 = AO2 + OD2
⇒ 172 = 82 + OD2
⇒ 289 = 64 + OD2
⇒ 225 = OD2
⇒ OD = 15
ومنه نستنتج أن طول القطر الثاني BD
BD = 2 × OD
= 2 × 15
= 30 cm
نستطيع الآن حساب مساحة المعين وفق العلاقة
S= (d1 × d2) / 2
S = 30 × 16 ÷ 2
S=240 cm2. [footnote]AREA OF RHOMBUS، من موقع: www.onlinemath4all.com، اطّلع عليه بتاريخ August/29/2020 | 02:45 PM[/footnote].
 TV
TV Partner With Us
Partner With Us